Let
Because in a standard Watson-Crick E0L system we
have only one table, we have to use other techniques to ensure
the possibility of introducing any pair ![]() in the first
phase and any pair
in the first
phase and any pair
![]() in the second one.
In order to do this, we have
in the second one.
In order to do this, we have ![]() sub-alphabets for the first phase,
where
sub-alphabets for the first phase,
where ![]() is the number of the pairs
is the number of the pairs ![]() . These alphabets
are in the form of
. These alphabets
are in the form of ![]() for
for
![]() and
and ![]() for
for
![]() . They are used in the following way:
we can modify the sentential form by introducing the pair
. They are used in the following way:
we can modify the sentential form by introducing the pair
![]() into it only during the two steps while the sentential form is rewritten
from a word over
into it only during the two steps while the sentential form is rewritten
from a word over ![]() into a word
into a word ![]() and from
a word over
and from
a word over ![]() into a word over
into a word over ![]() . In this two-step period
we can modify the sentential form according to
the current pair
. In this two-step period
we can modify the sentential form according to
the current pair ![]() or we can skip this possibility,
going on without altering the sentential form.
At the end of this process, that is,
when the sentential form is over
or we can skip this possibility,
going on without altering the sentential form.
At the end of this process, that is,
when the sentential form is over ![]() , we can continue the first
phase by rewriting the sentential form into a word
over
, we can continue the first
phase by rewriting the sentential form into a word
over ![]() or we can finish this
phase and start the second one with a word over
or we can finish this
phase and start the second one with a word over ![]() .
.
In the second phase we use the same technique: we have
![]() alphabets in the form of
alphabets in the form of ![]() for
for
![]() and
and
![]() for
for
![]() , where
, where ![]() is the number of
is the number of ![]() 's.
We can put the pair
's.
We can put the pair
![]() into the sentential form
during the two steps from
into the sentential form
during the two steps from ![]() to
to
![]() and from
and from
![]() to
to ![]() or
we can skip this possibility by not altering the sentential form during
these two steps.
At the end of this process (that is, when the sentential form is over
or
we can skip this possibility by not altering the sentential form during
these two steps.
At the end of this process (that is, when the sentential form is over
![]() ) we can
continue the second phase by the pair
) we can
continue the second phase by the pair
![]() or we can finish it by
rewriting the sentential form into a word over
or we can finish it by
rewriting the sentential form into a word over
![]() .
.
The last part of the derivation is analogous to the one used
in the previous section:
the checking is done through the alphabets
![]() ,
,
![]() ,
,
![]() . Only those words
. Only those words
![]() are generated for which there is a pair
are generated for which there is a pair
![]() whose members
are equal.
whose members
are equal.
As in the previous proof, for the sake of readability, we
use notations slightly different from the usual ones:
the complementary symbol of ![]() is
denoted by
is
denoted by
![]() and the complementary symbol of
and the complementary symbol of ![]() is denoted by
is denoted by
![]()
Let
![]() be the
standard Watson-Crick E0L system given as follows.
be the
standard Watson-Crick E0L system given as follows.
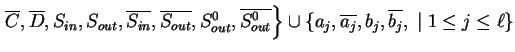 .
The symbols
.
The symbols
The terminal alphabet is
![]() and
the axiom is
and
the axiom is
![]()
Let us note here that it will follow from the construction of ![]() that
the sentential forms in any derivation
are either over
that
the sentential forms in any derivation
are either over
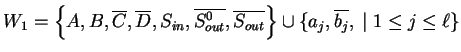 and
and
Due to these properties, in spite of the fact that we have only one table
in the system, we can use different sets of rules. By changing ![]() and
and
![]() we can decide which set is to be applied.
we can decide which set is to be applied.
Now we give the rules of ![]() for each alphabet, in the same order as they
are used in a derivation. This means that starting from
for each alphabet, in the same order as they
are used in a derivation. This means that starting from
![]() , we give all the rules of
, we give all the rules of ![]() which can be used
for rewriting the letters in the current alphabet
and a short explanation, too.
which can be used
for rewriting the letters in the current alphabet
and a short explanation, too.
First we give the rules used in the first phase.
If the sentential form is over ![]() for
for
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() ,
,
![]() ,
,
![]() , and
, and
![]() for the other letters
for the other letters ![]() .
.
In this step the system decides whether the current pair ![]() is to be introduced into the sentential form or not. Having
is to be introduced into the sentential form or not. Having
![]() in the sentential form implies that the pair is to be introduced, otherwise
the current pair is to be skipped. This decision can be made via
Watson-Crick complementarity in the following way.
In the sentential form all the purines but the symbol
in the sentential form implies that the pair is to be introduced, otherwise
the current pair is to be skipped. This decision can be made via
Watson-Crick complementarity in the following way.
In the sentential form all the purines but the symbol
![]() appear together with a
pyrimidine, thus, apart from
appear together with a
pyrimidine, thus, apart from ![]() ,
in the sentential form the number of purines and pyrimidines is
equal. By rewriting
,
in the sentential form the number of purines and pyrimidines is
equal. By rewriting ![]() to
to
![]() the number of
pyrimidines becomes greater than the number of purines,
thus each letter transforms into its complementary, that is,
the sentential form switches from
the number of
pyrimidines becomes greater than the number of purines,
thus each letter transforms into its complementary, that is,
the sentential form switches from ![]() to
to ![]() , or vice versa.
At the beginning of the derivation we have to distinguish the state
when no pairs
, or vice versa.
At the beginning of the derivation we have to distinguish the state
when no pairs ![]() have been introduced yet. During this state the symbol
have been introduced yet. During this state the symbol ![]() has a superscript 0, which disappears only when the first pair
has been represented in the sentential form. We can start the second
phase only when the symbol
has a superscript 0, which disappears only when the first pair
has been represented in the sentential form. We can start the second
phase only when the symbol ![]() does not have the superscript 0.
does not have the superscript 0.
If the sentential form is over ![]() for
for
![]() , then
the system has the following rules (in
the rules below
, then
the system has the following rules (in
the rules below ![]() and
and ![]() denote the lengths of
denote the lengths of ![]() and
and ![]() , and
, and
![]() and
and ![]() denote the values of
denote the values of ![]() and
and ![]() ):
):
![]() ,
,
![]() ,
,
![]() , and
, and
![]() for the other letters
for the other letters ![]() .
.
If at the beginning of this step the sentential form is over ![]() , then
the current pair
, then
the current pair ![]() is introduced by increasing the number of
is introduced by increasing the number of
![]() 's and
's and ![]() 's according to
's according to ![]() . Otherwise, the system does not
do anything but changes the indices of the letters.
. Otherwise, the system does not
do anything but changes the indices of the letters.
If the sentential form is over ![]() , then
the system has the following set of rules:
, then
the system has the following set of rules:
![]() ,
,
![]() ,
,
![]() , and
, and
![]() for the other letters
for the other letters ![]() .
.
Here the system decides whether to finish the first phase or to continue
it.
If the system makes the sentential form to be over
![]() , then
in the next step the system finishes the first phase, otherwise, when
the sentential form is over
, then
in the next step the system finishes the first phase, otherwise, when
the sentential form is over
![]() ,
it rewrites the sentential form into a word
over
,
it rewrites the sentential form into a word
over ![]() and thus the first
phase continues.
and thus the first
phase continues.
If the sentential form is over ![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() for
for ![]() ,
,
![]() for
for ![]() .
.
In the second phase we have similar rules and the working of the
system is the same as it was in the first phase: first the system
decides whether to put the current ![]() and
and ![]() into the
sentential form or not, then in the second step it works
according to this decision.
into the
sentential form or not, then in the second step it works
according to this decision.
If the sentential form is over ![]() for
for
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() ,
,
![]() , and
, and
![]() for the other letters
for the other letters ![]()
If the sentential form is over
![]() for
for
![]() , then
the system has the following rules (in the rules below
, then
the system has the following rules (in the rules below
![]() and
and ![]() denote the length and the value of
denote the length and the value of
![]() ):
):
![]() ,
,
![]()
![]() , and
, and
![]() for the other letters
for the other letters ![]()
If the sentential form is over
![]() , then the number of
, then the number of ![]() 's is
increased according to
's is
increased according to ![]() and
and ![]() is also introduced. Otherwise,
the sentential form is not altered, except the indices.
is also introduced. Otherwise,
the sentential form is not altered, except the indices.
If the sentential form is over
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() ,
,
![]() , and
, and
![]() for the other letters
for the other letters ![]()
Here the system decides whether to finish the second phase or
to continue it; this decision is done in the same way as
in the first phase.
If the sentential form is over
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() for
for ![]() ,
,
![]() for
for ![]() In the third phase we check whether the two parts of the pair represented
in the sentential form are equal or not.
It is done in an analogous way as in the construction
in Section 6.3. Therefore we give the rules without
any further explanation.
In the third phase we check whether the two parts of the pair represented
in the sentential form are equal or not.
It is done in an analogous way as in the construction
in Section 6.3. Therefore we give the rules without
any further explanation.
If the sentential form is over
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
for
,
for
![]() ,
,
![]() and
and
![]() for the other letters
for the other letters ![]()
If the sentential form is over
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() ,
,
![]() ,
,
![]() ,
,
![]() for
for
![]() , and
, and
![]() for the other letters
for the other letters ![]()
If the sentential form is over
![]() , then
the system has the following rules:
, then
the system has the following rules:
![]() ,
,
![]() ,
,
![]() ,
,
![]() for
for
![]() , and
, and
![]() for the other letters
for the other letters ![]()
To make the set ![]() complete, we also add the rules
complete, we also add the rules
![]() for
for
![]() .
The construction guarantees that the
system
.
The construction guarantees that the
system ![]() generates the language
generates the language ![]() because of the following
reasons:
because of the following
reasons:
1. All the words of ![]() can be generated according to the
representation given by Theorem 6.3: in the first two phases
the pairs
can be generated according to the
representation given by Theorem 6.3: in the first two phases
the pairs ![]() , the words
, the words ![]() and also the symbols
and also the symbols ![]() are introduced into the sentential form, while in the third phase the checking
deletes all non-terminal symbols.
are introduced into the sentential form, while in the third phase the checking
deletes all non-terminal symbols.
2. Only those words can be generated which
have a representation given in Theorem 6.3, because
otherwise the system introduces symbols ![]() , and thus the derivation is
blocked.height 5pt width 5pt depth 0pt
, and thus the derivation is
blocked.height 5pt width 5pt depth 0pt
We note that, unlike the construction presented in Section 6.3,
the above proof
uses Watson-Crick complementarity in the first and the second
phase as well. Furthermore, non-determinism appears only in these two phases.
As mentioned above,
with a slight modification of the system ![]() we can
give another construction which shows
that
standard Watson-Crick EDT0L systems can generate all recursively enumerable
languages.
we can
give another construction which shows
that
standard Watson-Crick EDT0L systems can generate all recursively enumerable
languages.
The first sub-set contains the rules rewriting a purine ![]() to a
purine;
the second sub-set contains the other rules, that is,
those switching a purine
to a
purine;
the second sub-set contains the other rules, that is,
those switching a purine ![]() to a pyrimidine.
Hence, the system can use the first table if it does not want to switch the
sentential form into its complementary word, otherwise
it uses the second table.
This modification does not affect the generated language; the new system works
in the same way as the system defined in Theorem 6.5.
Therefore for every recursively enumerable
language we can give a standard Watson-Crick EDT0L system with only
two tables. height 5pt width 5pt depth 0pt
to a pyrimidine.
Hence, the system can use the first table if it does not want to switch the
sentential form into its complementary word, otherwise
it uses the second table.
This modification does not affect the generated language; the new system works
in the same way as the system defined in Theorem 6.5.
Therefore for every recursively enumerable
language we can give a standard Watson-Crick EDT0L system with only
two tables. height 5pt width 5pt depth 0pt
Let us note here that in this EDT0L system the number of tables is only two,
but the number of non-terminals depends on ![]() and
and ![]() , given by
the EPC representation of
, given by
the EPC representation of ![]() .
.