In this part of the chapter we introduce standard
Watson-Crick eco-grammar systems
and we show that for any recursively enumerable language ![]() we can
construct a standard Watson-Crick eco-grammar system generating it.
Furthermore, in this standard Watson-Crick eco-grammar system there is only
one agent and the set of the environment is deterministic.
we can
construct a standard Watson-Crick eco-grammar system generating it.
Furthermore, in this standard Watson-Crick eco-grammar system there is only
one agent and the set of the environment is deterministic.
The derivation goes in the same way as in an extended simple EG system, the only difference is that whenever a word with more pyrimidines than purines would be derived, a complementary transition takes place.
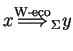 ), if
), if
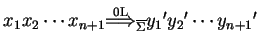 holds with the
E0L system
holds with the
E0L system
Informally speaking, in a derivation step first each agent chooses one position to apply a rule, then the remaining letters are rewritten by the environment. If after this rewriting the word contains more pyrimidines than purines, then all letters turn into their complementary letter and the derivation continues from this word, otherwise the derivation continues without a complementary transition.
We denote the
transitive and reflexive closure of
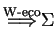 by
by
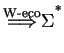 .
.
The generated language consists of the words over
![]() which can be obtained from the axiom in some derivation steps:
which can be obtained from the axiom in some derivation steps:
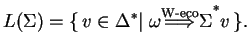
Now we give a standard Watson-Crick eco-grammar system, as an example, and show that although the system contains only one agent and its rules are simple, it is able to generate a non-ET0L language (the same as in Example 5.10 and 6.1).
The working of the system is divided into three phases. In the first phase
the agent uses several times the rule
![]()
![]() and
the environment does not alter anything. In this way
the sentential form becomes a word in the form
and
the environment does not alter anything. In this way
the sentential form becomes a word in the form
![]() , with
, with
![]() .
When finally the agent uses the rule
.
When finally the agent uses the rule
![]()
![]() ,
a word with more pyrimidines than purines would be generated, thus a
complementary transition takes place and the word
,
a word with more pyrimidines than purines would be generated, thus a
complementary transition takes place and the word
![]() results.
Then the agent rewrites
results.
Then the agent rewrites ![]() to
to
![]() and the environment changes the indices from 0 to 1 and rewrites
the letters into their complementary symbols. Hence the sentential form
becomes
and the environment changes the indices from 0 to 1 and rewrites
the letters into their complementary symbols. Hence the sentential form
becomes
![]() .
.
At this point the only rule which is available
for the agent is
![]() . While the agent rewrites the letters
. While the agent rewrites the letters ![]() to letters
to letters ![]() , the environment writes words
, the environment writes words
![]() before the letters
before the letters ![]() . This can
happen at most
. This can
happen at most ![]() times, because
after this the agent cannot work, the derivation
is blocked. At the
times, because
after this the agent cannot work, the derivation
is blocked. At the ![]() th iteration of this step,
at most in the
th iteration of this step,
at most in the ![]() th step, the environment must use the rule
th step, the environment must use the rule
![]() , which results in a complementary transition and the
sentential form becomes a word in the form of
, which results in a complementary transition and the
sentential form becomes a word in the form of
![]()
![]() .
.
From this point the derivation is finished in one step:
the agent deletes the symbol ![]() , the environment deletes all letters,
except the letters
, the environment deletes all letters,
except the letters
![]() and
and
![]() ,
which are rewritten into terminal form.
,
which are rewritten into terminal form.
In this way all the words in the form of
![]() , with
, with
![]() can be
generated and it is clear from the construction that
the working explained above is the only possibility to generate a
terminal word.
can be
generated and it is clear from the construction that
the working explained above is the only possibility to generate a
terminal word.
This example shows how a standard
Watson-Crick eco-grammar system works and illustrates
the power of these systems as well.
Let us note that in this example the environment is not deterministic,
there are two rules for the symbol ![]() . The construction of the
following theorem prove that we could avoid this non-determinism:
all recursively
enumerable language can be generated by standard
Watson-Crick eco-grammar systems
with only one agent, and with a deterministic environment.
. The construction of the
following theorem prove that we could avoid this non-determinism:
all recursively
enumerable language can be generated by standard
Watson-Crick eco-grammar systems
with only one agent, and with a deterministic environment.
The set of the agent, ![]() , contains all the
, contains all the ![]() rewriting rules of
rewriting rules of ![]() where
where ![]() is in the form of
is in the form of
![]() or
or ![]() with
with
![]() ,
,
![]() ,
and
,
and
![]() . Moreover, in order to guarantee that
the agent could work in the last two steps
(if the sentential form is not empty), we also
put the following rules into
. Moreover, in order to guarantee that
the agent could work in the last two steps
(if the sentential form is not empty), we also
put the following rules into
![]() :
:
![]() ,
,
![]() .
.
It is clear from the construction of
![]() that
it works in the same way as
that
it works in the same way as ![]() in Theorem 6.5;
the only difference is that the choices are made by the agent, not by the
E0L set. Thus
in Theorem 6.5;
the only difference is that the choices are made by the agent, not by the
E0L set. Thus
![]() , which completes the proof.height 5pt width 5pt depth 0pt
, which completes the proof.height 5pt width 5pt depth 0pt