An extended tabled simple eco-grammar system
-
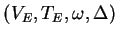 is an ET0L system,
is an ET0L system,
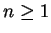 , and
, and
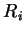 is a non-empty set of CF rules over
is a non-empty set of CF rules over 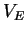 for
for
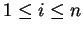 .
.
In this section extended tabled simple eco-grammar systems are investigated. In such a system the environment can be represented by more than one 0L system.
Here ![]() ,
, ![]() ,
, ![]() (for
(for
![]() ),
), ![]() and
and ![]() have
the same meaning as in Definition 2.4,
that is,
these are the alphabet of the system, the number of the agents,
the production sets representing
the agents, the axiom, and the terminal alphabet.
have
the same meaning as in Definition 2.4,
that is,
these are the alphabet of the system, the number of the agents,
the production sets representing
the agents, the axiom, and the terminal alphabet.
![]() is the set of
tables of the environment, where each
is the set of
tables of the environment, where each ![]() is a complete set of CF rules over
is a complete set of CF rules over
![]() .
.
In an extended tabled simple
eco-grammar system the environment in each derivation step
can choose a table to perform a parallel rewriting.
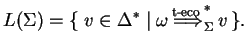
We show that the generated language of this system is
Before this step, when ![]() and
and ![]() disappear from the
sentential form, in every step the agent has to use the
rule
disappear from the
sentential form, in every step the agent has to use the
rule
![]() , or otherwise the environment introduces a
, or otherwise the environment introduces a ![]() ,
and the environment has to use the first table
,
and the environment has to use the first table ![]() , or otherwise
, or otherwise
![]() would be rewritten to
would be rewritten to ![]() .
Thus either the derivation is
.
Thus either the derivation is
![]() , or
the first few steps are
, or
the first few steps are
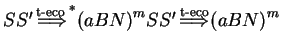 .
After these steps the only possibility for the agent is to
use rule the
.
After these steps the only possibility for the agent is to
use rule the
![]() . During these
steps the environment can use any of its tables, therefore it can introduce
letters
. During these
steps the environment can use any of its tables, therefore it can introduce
letters ![]() before all the
before all the ![]() 's or it can rewrite either all
letters
's or it can rewrite either all
letters ![]() to
to ![]() or all letters
or all letters ![]() to
to ![]() .
Because there are only
.
Because there are only ![]() symbols
symbols ![]() in the
sentential form, the derivation lasts exactly
in the
sentential form, the derivation lasts exactly ![]() more
steps. Hence at the end
of the derivation, when there are no more
more
steps. Hence at the end
of the derivation, when there are no more ![]() symbols left, there are
at least one but at most
symbols left, there are
at least one but at most ![]() symbols
symbols ![]() after each
after each ![]() .
.
The above explication shows
that all non-empty generated words are in the form
![]() ,
,
![]() .
It follows from the construction that all words of this form and
the
empty word,
.
It follows from the construction that all words of this form and
the
empty word, ![]() , too,
are in the generated language, which is thus indeed:
, too,
are in the generated language, which is thus indeed:
This example shows that even a very simple
extended tabled simple eco-grammar system
with only one agent is able to produce a quite complicated language,
namely a language which is not an ET0L one (see [Rozenberg and SalomaaRozenberg and
Salomaa1980]).
We show that these systems can generate all recursively enumerable
languages. This result is a direct consequence of the following lemma.
We denote by ![]() the number of rules in
the number of rules in ![]() and by
and by ![]() the set
the set
![]() .
The rules of
.
The rules of ![]() are enumerated as
are enumerated as
![]() .
We will refer to the components of the
.
We will refer to the components of the ![]() th rule as
th rule as ![]() ,
,
![]() ,
,
![]() , and
, and ![]() .
.
Now we will construct an extended tabled simple eco-grammar system
![]() ,
such that
,
such that
![]() Let
Let
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where |
|
|
|
|
|
|
|
|
|
|
|
|
for |
|
|
|
|
|
|
|
|
|
|
|
|
|
for |
|
|
|
|
|
|
|
for |
|
|
|
|
|
|
|
|
|
|
|
Those symbols which are not mentioned above in the tables are
rewritten into ![]() ; these rules make the tables complete.
; these rules make the tables complete.
We introduce different alphabets according to the rules of ![]() in
the following way. These alphabets are
versions of
in
the following way. These alphabets are
versions of ![]() with different indexes:
for the
with different indexes:
for the ![]() th rule of
th rule of ![]() we have alphabets
we have alphabets
![]() and
and
![]() .
Moreover, we have some special additional symbols
in the ETEG system in order to
coordinate the derivation. These are
.
Moreover, we have some special additional symbols
in the ETEG system in order to
coordinate the derivation. These are
![]() .
By
.
By ![]() the derivation is blocked: if this symbol appears,
then the derivation never results
in a terminal word.
The different versions of symbol
the derivation is blocked: if this symbol appears,
then the derivation never results
in a terminal word.
The different versions of symbol ![]() allow the agent to work
when
allow the agent to work
when
![]() .
.
First we show how a derivation step of ![]() can be simulated by
can be simulated by
![]() . During the simulation the sentential form has the form
. During the simulation the sentential form has the form ![]() ,
where the word
,
where the word ![]() corresponds to the sentential form of
corresponds to the sentential form of ![]() , and
, and
![]() and
and ![]() coordinate the simulation.
Let us suppose that in a derivation step the rule
coordinate the simulation.
Let us suppose that in a derivation step the rule
![]() is used for a sentential form
is used for a sentential form ![]() .
The simulation in the ETEG system goes as follows.
.
The simulation in the ETEG system goes as follows.
In the first step the environment applies table ![]() to
rewrite
to
rewrite ![]() into
into
![]() or into
or into
![]() depending on whether or not
depending on whether or not
![]() ;
the agent rewrites
;
the agent rewrites
![]() into
into ![]() . This is the only role of
. This is the only role of ![]() : it allows
the agent to work during the first step
of the simulation.
: it allows
the agent to work during the first step
of the simulation.
In the second step the agent applies the rule
![]() if
if
![]() or applies the rule
or applies the rule
![]() if
if ![]() .
The environment rewrites the remaining letters by using table
.
The environment rewrites the remaining letters by using table
![]() .
.
In the third simulation step the agent applies its rule corresponding
to the rule of ![]() , namely the rule
, namely the rule
![]() ,
while the environment rewrites the remaining letters
by using table
,
while the environment rewrites the remaining letters
by using table ![]() . During this last step, the environment can
delete the special symbols
. During this last step, the environment can
delete the special symbols ![]() and
and ![]() , thus allowing
the possibility of finishing the derivation if the sentential form would
be a terminal word.
, thus allowing
the possibility of finishing the derivation if the sentential form would
be a terminal word.
Now we have showed that we can simulate the derivation steps of
the random-context grammar.
It follows from the construction of the simulating ETEG system that
the behaviour described above is the only one which can result in
a terminal word. The only possibility to start a derivation from a word
over
![]() is to use one of the tables
is to use one of the tables ![]() and the rule
and the rule
![]() of
the agent.
If the sentential form contains some forbidding letters from
of
the agent.
If the sentential form contains some forbidding letters from ![]() ,
then the environment blocks the derivation in the next
step by introducing a
,
then the environment blocks the derivation in the next
step by introducing a ![]() ; if
the permitting symbol of the non-empty set
; if
the permitting symbol of the non-empty set ![]() does not appear in the sentential form, the
derivation is blocked because the agent cannot work.
(It cannot use
the other rule
does not appear in the sentential form, the
derivation is blocked because the agent cannot work.
(It cannot use
the other rule
![]() , because this symbol appears
in the sentential form only if
, because this symbol appears
in the sentential form only if
![]() .) In the next step the agent
has to use the rule
.) In the next step the agent
has to use the rule
![]() and the environment
has to use table
and the environment
has to use table ![]() . These three consecutive steps
simulate the application of one of the rules of
. These three consecutive steps
simulate the application of one of the rules of ![]() . height 5pt width 5pt depth 0pt
. height 5pt width 5pt depth 0pt
Using the fact that
![]() we obtain the following theorem:
we obtain the following theorem: