


Next: Watson-Crick systems
Up: Generative power of variants
Previous: Extended tabled simple eco-grammar
Contents
In this section another variant of extended simple eco-grammar
systems is studied: the weak extended simple eco-grammar system.
This variant has the
same components as an extended simple eco-grammar system but it works
in a different way.
Definition 5.13
A weak extended simple eco-grammar system (a wEEG system, for short) is
a construct
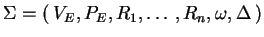
, where
all the components
are the same as in Definition
2.4.
In a weak extended simple eco-grammar system
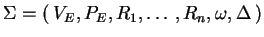
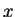
directly derives
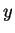
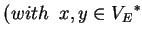
, written as
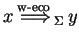
),
if
-
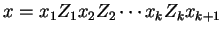 , with
, with
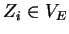 ,
,
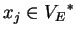 ,
,
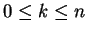 ,
,
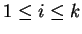 , and
, and
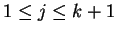 ,
,
-
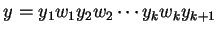 , with
, with
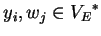 ,
,
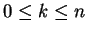 ,
,
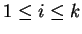 , and
, and
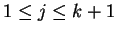 ,
,
- there exists a permutation of some agents, namely
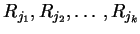 , such that
, such that
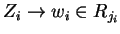 for
for
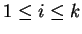 ,
,
-
dom
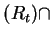 alph
alph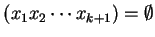 ,
for
,
for
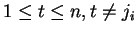 ,
,
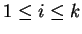 and
and
-
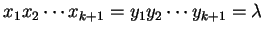 or
or
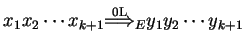 ,
where
,
where
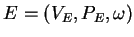 is the
0L system of the environment.
is the
0L system of the environment.
We denote by
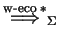 the transitive and reflexive closure of
the transitive and reflexive closure of
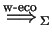 .
.
Informally speaking, in a weak extended simple eco-grammar system we choose
some agents to perform a common action in the following
way: the chosen agents can perform an action together
and there is no
symbol among the remaining letters where any of the other agents
could act. The chosen agents perform their actions, the remaining
letters are rewritten by the environment.
In that particular case when there is only one agent
in the system, this definition
implies that the agent has to work if it is able to but if
no letter can be rewritten by the agent, then it is the environment itself
that continues the derivation.
Definition 5.14
For a weak extended simple eco-grammar system
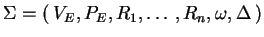
the generated language is the following:
In the following we show that wEEG systems can generate all recursively enumerable
languages.
The result is based on the following lemma.
Lemma 5.15
Let
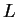
be a language in
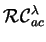
.
Then there
exists a weak extended simple eco-grammar system
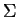
with one
agent, such that
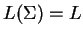
.
PROOF.
Let 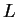 be a language in
be a language in
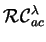 .
As in Lemma 5.11, we can suppose that
.
As in Lemma 5.11, we can suppose that 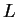 can be generated
by a a random-context grammar with complete
checking
can be generated
by a a random-context grammar with complete
checking
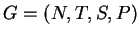 , where
the rules in
, where
the rules in 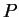 have
the form
have
the form
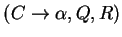 , with
, with 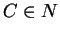 ,
,
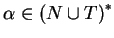 ,
card
,
card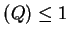 , and
card
, and
card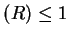 .
By the note at the end of the proof
of Lemma 5.6, we can assume that there are no rules with
.
By the note at the end of the proof
of Lemma 5.6, we can assume that there are no rules with
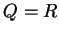 ,
, 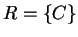 or
or 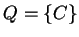 .
We will give a weak extended simple eco-grammar system
.
We will give a weak extended simple eco-grammar system
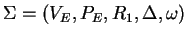 , such that
, such that
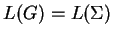 .
.
We present the definition of this system 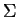 and
explain its functioning. Similar to Lemma 5.11,
the notation
and
explain its functioning. Similar to Lemma 5.11,
the notation 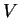 stands for
stands for 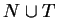 ,
, 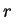 denotes the number
of rules in
denotes the number
of rules in 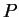 , the rules in
, the rules in 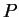 are enumerated as
are enumerated as
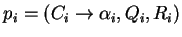 .
.
Let
The main point of the simulation is that we
simulate the application of the rules in their order from 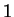 to
to 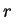 , each
time either simulating the rule or skipping it.
After having simulated or skipped the
, each
time either simulating the rule or skipping it.
After having simulated or skipped the 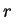 th rule we continue
with the first one.
th rule we continue
with the first one.
We do the simulation of a rule by introducing five different alphabets
for each rule of 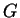 : for the
: for the 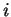 th rule we introduce the alphabets
th rule we introduce the alphabets
![$ [V,i,j]$](img32.gif) for
for
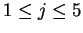 . We start the simulation or the skipping
of the
. We start the simulation or the skipping
of the 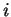 th rule with a word over
the alphabet
th rule with a word over
the alphabet ![$ [V,i-1,5]$](img1088.gif) , then during the simulation
we go through the alphabets
, then during the simulation
we go through the alphabets ![$ [V,i,j]$](img32.gif) for
for
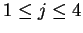 , and
finish with a word over the alphabet
, and
finish with a word over the alphabet ![$ [V,i,5]$](img1090.gif) . Consequently we can
finish the whole derivation or we can continue with the next rule.
. Consequently we can
finish the whole derivation or we can continue with the next rule.
There are more additional alphabets for coordinating the simulation:
the letters ![$ [Z,i,j]$](img1091.gif) and
and
![$ [\widehat{Z},i,k]$](img1092.gif) for
for
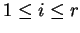 ,
,
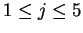 , and
, and
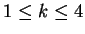 make
it possible to skip the
make
it possible to skip the 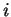 th rule of
th rule of 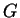 ; the symbols
; the symbols
![$ [{\widehat{C}}_i,i,k]$](img1094.gif) let the agent simulate the
let the agent simulate the 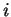 th rule of
th rule of 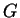 ;
the symbols
;
the symbols
![$ [U,i,{\ell}]$](img1095.gif) are introduced only if
are introduced only if
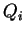 , the permitting set is empty and
make it
possible to deal with this case;
the symbols
, the permitting set is empty and
make it
possible to deal with this case;
the symbols ![$ [K,i,3]$](img1096.gif) ensure that the derivation
is blocked if the agent simulates the
ensure that the derivation
is blocked if the agent simulates the 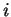 th
rule of
th
rule of 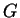 while the non-empty permitting condition is missing.
while the non-empty permitting condition is missing.
In the following, we first show how the application of a rule of 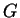 can
be simulated and we also show how the application can be skipped.
Then we
show why the construction of the above wEEG system guarantees that
only those derivations result in a terminal word which follow
a derivation of the random-context grammar
can
be simulated and we also show how the application can be skipped.
Then we
show why the construction of the above wEEG system guarantees that
only those derivations result in a terminal word which follow
a derivation of the random-context grammar 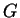 .
.
Let us suppose that we want to simulate the application of the
first rule
of 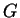 :
:
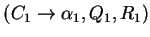 (the case of the other rules
is similar) and
let us first suppose that
(the case of the other rules
is similar) and
let us first suppose that
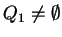 . Before the simulation
the sentential form in
. Before the simulation
the sentential form in 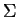 is over
is over
![$ \{[W,r,5]\;\vert\;
W\in V\cup\{Z\}\}$](img1099.gif) .
.
In the first step the agent ``decides'' whether the current rule
(in this case the first rule of 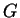 ) will be simulated or
will be skipped. Let us suppose that the rule is to be simulated.
In this case the agent uses the
rule
) will be simulated or
will be skipped. Let us suppose that the rule is to be simulated.
In this case the agent uses the
rule
![$ [C_1,r,5]\ensuremath{\rightarrow}[{\widehat{C}}_1,1,1]$](img1100.gif) . The other letters
are rewritten by the environment, using the rules
. The other letters
are rewritten by the environment, using the rules
![$ \{[X,r,5]\ensuremath{\rightarrow}[X,1,1]\;\vert\;X\in V\cup \{Z\}\}$](img1101.gif) .
.
In the next step the agent checks whether or not the forbidding context
is present in the sentential form. This is done in the following
way: the agent introduces a 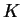 if
if ![$ [B,1,1]$](img1102.gif) is present (where
is present (where
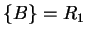 is the forbidding context),
while otherwise the agent does not work because
is the forbidding context),
while otherwise the agent does not work because
![$ [\widehat{Z},1,1]$](img1104.gif) is
not present in the sentential form.
The environment increases the second index of the symbols
from 1 to 2 in this step.
is
not present in the sentential form.
The environment increases the second index of the symbols
from 1 to 2 in this step.
In the third step the agent uses the rule
![$ [A,1,2]\ensuremath{\rightarrow}[A,1,3][K,1,3]$](img1105.gif) for
for 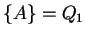 ; the environment increases the
second indexes from 2 to 3 in the other symbols.
; the environment increases the
second indexes from 2 to 3 in the other symbols.
In the fourth step the agent deletes ![$ [K,1,3]$](img1107.gif) while the
environment increases the second indexes from 3 to 4.
In the fifth and final step the agent applies the rule
while the
environment increases the second indexes from 3 to 4.
In the fifth and final step the agent applies the rule
![$ [{\widehat{C}}_1,1,4]\ensuremath{\rightarrow}[{\alpha}_1,1,5]$](img1108.gif) or the rule
or the rule
![$ [{\widehat{C}}_1,1,4]\ensuremath{\rightarrow}\lambda$](img1109.gif) , which correspond
to the first rule of
, which correspond
to the first rule of  ; the environment increases
the second indexes.
Therefore we obtain a word over
; the environment increases
the second indexes.
Therefore we obtain a word over
![$ \{[W,1,5]\;\vert\;W\in V\cup \{Z\}\}$](img1110.gif) .
.
If
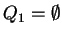 , that is, when the permitting condition is empty, then the
simulation is different. While the environment does the same
as in the previous case, the agent applies different rules.
The rule the agent uses in the first step is
, that is, when the permitting condition is empty, then the
simulation is different. While the environment does the same
as in the previous case, the agent applies different rules.
The rule the agent uses in the first step is
![$ [C_1,r,5]\ensuremath{\rightarrow}[{\widehat{C}}_1,1,1][U,1,1]$](img1112.gif) and thus
and thus ![$ [U,1,1]$](img1113.gif) is introduced.
In the third step this symbol is used to introduce
is introduced.
In the third step this symbol is used to introduce ![$ [K,1,3]$](img1107.gif) and from that point the simulation continues in the same way as
described above, that is, when
and from that point the simulation continues in the same way as
described above, that is, when
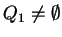 .
.
Now we show how we can do the skipping of the first rule (the case of
the other rules is the same). Let us suppose
again that we have a word over the alphabet
![$ \{[W,r,5]\;\vert\;
W\in V\cup\{Z\}\}$](img1099.gif) .
.
The environment works in the same way as it did
in the previous case, the
difference is in the behaviour of the agent.
In the first step the agent chooses the rule
![$ [Z,r,5]\ensuremath{\rightarrow}[\widehat{Z},1,1]$](img1114.gif) , in the next step the rule
, in the next step the rule
![$ [\widehat{Z},1,1]\ensuremath{\rightarrow}[\widehat{Z},1,2]$](img1115.gif) , and in the third step the rule
, and in the third step the rule
![$ [\widehat{Z},1,2]\ensuremath{\rightarrow}[\widehat{Z},1,3]$](img1116.gif) . In the fourth and in the
fifth step
the agent no longer has any rule to apply, hence it does not perform any
action.
By the end of these five steps we have the same word as we had before,
apart from the first indexes in the symbols: we have the same word over
the alphabet
. In the fourth and in the
fifth step
the agent no longer has any rule to apply, hence it does not perform any
action.
By the end of these five steps we have the same word as we had before,
apart from the first indexes in the symbols: we have the same word over
the alphabet
![$ \{[W,1,5]\;\vert\;W\in V\cup \{Z\}\}$](img1110.gif) .
.
At this point the simulation or the skipping
of the second rule can start and can be carried out in the previous
manner.
We can continue this process until the last rule, the 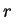 th one, when we
can restart
the whole procedure with the first rule again.
th one, when we
can restart
the whole procedure with the first rule again.
In order to finish the derivation,
after having finished the simulation of a rule of 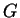 the agent chooses
the rule in the form of
the agent chooses
the rule in the form of
![$ [Z,i,5]\ensuremath{\rightarrow}\lambda$](img1117.gif) while the
environment rewrites the remaining letters according to its rules
while the
environment rewrites the remaining letters according to its rules
![$ [X,i,5]\ensuremath{\rightarrow}X$](img1118.gif) .
Thus we have seen that
.
Thus we have seen that
In the following we show that the eco-grammar system must follow
one of the sequences presented above,
or otherwise the derivation would never
terminate.
In the first step, when the sentential form is over ![$ [W,i-1,5]$](img1120.gif) ,
the agent can work because either the left-hand side of the
current rule of
,
the agent can work because either the left-hand side of the
current rule of 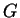 is present
(and thus the agent can rewrite
is present
(and thus the agent can rewrite
![$ [C_i,i-1,5]$](img1121.gif) ) or the symbol
) or the symbol ![$ [Z,i-1,5]$](img1122.gif) can be rewritten.
(At the end of the proof we explain why we can suppose that
can be rewritten.
(At the end of the proof we explain why we can suppose that 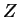 has not yet disappeared from the sentential form.)
has not yet disappeared from the sentential form.)
Therefore, in this first step the agent marks a position where it can perform
the application
of the current rule or it can mark 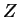 .
If it marks a position for the current rule, then in the next steps
it must check the appearance of the forbidding and the permitting
context. The derivation can result in a word not containing letters
.
If it marks a position for the current rule, then in the next steps
it must check the appearance of the forbidding and the permitting
context. The derivation can result in a word not containing letters 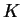 only if the check is successful.
This is done in the following way: the derivation is
blocked by the rule
only if the check is successful.
This is done in the following way: the derivation is
blocked by the rule
![$ [B,i,1]\ensuremath{\rightarrow}K$](img1123.gif) if the forbidding context is present, or by the rule
if the forbidding context is present, or by the rule
![$ [{\widehat{C}}_i,i,3]\ensuremath{\rightarrow}K$](img1124.gif) if the non-empty
permitting condition is missing.
In the last step the agent must apply the rule corresponding
to the rule of
if the non-empty
permitting condition is missing.
In the last step the agent must apply the rule corresponding
to the rule of 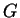 .
.
Thus we have seen that if the agent decides to mark a position for applying
the current rule, then it must check whether or not
the rule is applicable,
and, if the checking is successful, then finally
it must simulate it.
If the agent chooses the other possibility and marks 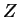 ,
then in the next two steps he must increase the second index of
,
then in the next two steps he must increase the second index of
![$ [\widehat{Z},i,j]$](img1125.gif) from 1 to 2 and from 2 to 3.
In the next two steps the agent cannot work.
Hence if the agent chooses to mark
from 1 to 2 and from 2 to 3.
In the next two steps the agent cannot work.
Hence if the agent chooses to mark ![$ [Z,i,5]$](img1126.gif) , then
the work of the whole
system follows the strategy of skipping the current rule, or otherwise the
derivation would be blocked.
, then
the work of the whole
system follows the strategy of skipping the current rule, or otherwise the
derivation would be blocked.
As far as the end of the derivation is concerned, the
environment
has to apply the rules in the form of
![$ [X,i,5]\ensuremath{\rightarrow}X$](img1118.gif) for all
the letters in the same derivation step, or
otherwise the derivation is blocked in the next step.
It can happen that the agent deletes
for all
the letters in the same derivation step, or
otherwise the derivation is blocked in the next step.
It can happen that the agent deletes 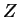 before
the end of the derivation but this fact does not allow any new
word to be generated, so we can safely assume that the deletion of
before
the end of the derivation but this fact does not allow any new
word to be generated, so we can safely assume that the deletion of 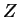 happens
in the same derivation step as the rewritings
happens
in the same derivation step as the rewritings
![$ [X,i,5]\ensuremath{\rightarrow}X$](img1118.gif) .
We have seen the other direction of the inclusion,
.
We have seen the other direction of the inclusion,
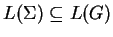 , which completes the proof of the lemma.height 5pt width 5pt depth 0pt
, which completes the proof of the lemma.height 5pt width 5pt depth 0pt
Because
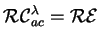 ,
we obtain the
following theorem:
,
we obtain the
following theorem:
Theorem 5.16
Let
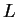
be a recursively enumerable language.
Then there
exists a weak extended simple eco-grammar system
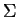
with one
agent, such that
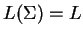
.



Next: Watson-Crick systems
Up: Generative power of variants
Previous: Extended tabled simple eco-grammar
Contents
Csima Judit
2002-01-04
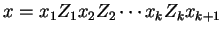 , with
, with
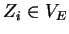 ,
,
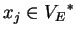 ,
,
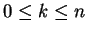 ,
,
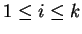 , and
, and
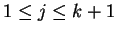 ,
,
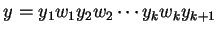 , with
, with
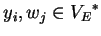 ,
,
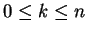 ,
,
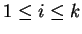 , and
, and
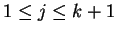 ,
,
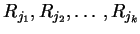 , such that
, such that
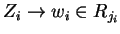 for
for
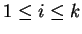 ,
,
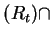 alph
alph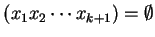 ,
for
,
for
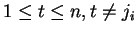 ,
,
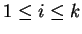 and
and
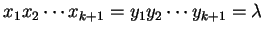 or
or
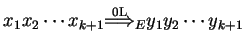 ,
where
,
where
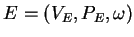 is the
0L system of the environment.
is the
0L system of the environment.