A simple eco-grammar system (a simple EG system, for short) is a construct
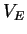 is a finite, non-empty alphabet,
is a finite, non-empty alphabet,
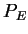 is a complete set of CF rules over
is a complete set of CF rules over 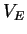 ,
,
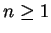 ,
,
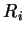 is a non-empty set of CF rules over
is a non-empty set of CF rules over 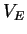 for
for
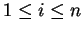 , and
, and
-
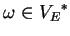 .
.
We give only the definition of simple eco-grammar systems. The formal definition of the original (i.e. non-simple) version, which was introduced in [Csuhaj-Varjú, Kelemen, Kelemenová, and PaunCsuhaj-Varjú et al.1997] is not presented, because in this dissertation we study only simple eco-grammar systems. For more details about the original version see [Csuhaj-Varjú, Kelemen, Kelemenová, and PaunCsuhaj-Varjú et al.1997].
The system changes its state by a simultaneous action of the agents
and by a parallel rewriting done according to ![]() :
in each derivation
step first each agent rewrites one letter in the sentential form,
then the environment rewrites the remaining letters in a
parallel way.
:
in each derivation
step first each agent rewrites one letter in the sentential form,
then the environment rewrites the remaining letters in a
parallel way.
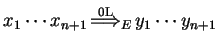 where
where
Let us note here that according to this definition, all the agents have to work in each derivation step. In [ter Beekter Beek1999] and in Chapter 5 another version of simple eco-grammar systems is studied, the so called weak simple eco-grammar system. In this case the derivation is not blocked if some of the agents cannot perform any action on the sentential form.
We denote the transitive and reflexive closure of
![]() by
by
![]() .
The generated language consists of all the words which can be derived from the
initial string.
.
The generated language consists of all the words which can be derived from the
initial string.
The extended version of simple eco-grammar systems, where a subset of the alphabet, called the terminal alphabet is distinguished, was introduced in [Csuhaj-Varjú, Kelemen, Kelemenová, and PaunCsuhaj-Varjú et al.1997].
In an extended simple eco-grammar system, the derivation goes in the same way as presented in Definition 2.2, the only difference is that the generated language contains only words over the terminal alphabet.
Now we present two examples which illustrates our model and its power.
When deriving a terminal word, in a derivation step we have only three possibilities: we can use the first rules of the agents together or we can use the second ones or the third ones, otherwise the derivation is blocked because in the next step one of the agents could not work. Therefore either all the agents introduces the same letter