A 0L system is a triplet
![]() , where
, where ![]() is a
finite alphabet,
is a
finite alphabet, ![]() is a set of context-free rules over
is a set of context-free rules over ![]() , and
, and
![]() is the axiom.
Moreover,
is the axiom.
Moreover, ![]() has to be complete, that is, for each symbol
has to be complete, that is, for each symbol ![]() in
in ![]() there must be at least one rule
there must be at least one rule
![]() in
in ![]() with this letter
with this letter ![]() on the left-hand side.
on the left-hand side.
0L systems use parallel derivations: we say that ![]() directly derives
directly derives
![]() in a 0L system
in a 0L system
![]() , with
, with
![]() ,
written as
,
written as
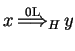 , if
, if
![]() ,
,
![]() ,
where
,
where ![]() ,
,
![]() ,
and the rules
,
and the rules
![]() are in
are in ![]() for
for
![]() .
.
A T0L system is a triplet
![]() , where
, where ![]() is a
finite alphabet,
is a
finite alphabet,
![]() is a finite
set of tables over
is a finite
set of tables over ![]() , where each table
, where each table ![]() for
for
![]() is a complete set of CF rules over
is a complete set of CF rules over ![]() , and
, and
![]() is the axiom.
We say that
is the axiom.
We say that ![]() directly derives
directly derives
![]() in a T0L system
in a T0L system
![]() , with
, with
![]() , written as
, written as
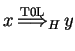 , if
, if
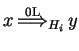 for some
for some ![]() ,
,
![]() ,
with the 0L system
,
with the 0L system
![]() .
.
An ET0L system is a quadruple
![]() , where
, where
![]() is a T0L system, and
is a T0L system, and
![]() is a subset of
is a subset of ![]() , the
terminal alphabet.
In an ET0L system
, the
terminal alphabet.
In an ET0L system
![]()
![]() directly derives
directly derives
![]() , with
, with
![]() , written as
, written as
 , if
, if
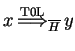 .
.
The transitive and reflexive closure of
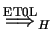 is denoted by
is denoted by
![]() .
The generated language of the ET0L system
.
The generated language of the ET0L system ![]() (denoted by
(denoted by ![]() )
is
)
is
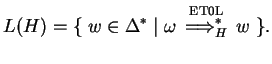
T0L and 0L systems are special cases of ET0L systems:
![]() stands in both cases; moreover, in the case of 0L systems
stands in both cases; moreover, in the case of 0L systems
![]() also holds. In an E0L system there is only one table but
also holds. In an E0L system there is only one table but
![]() is not necessarily equal to
is not necessarily equal to ![]() .
Therefore the above definition gives the generated language for these
systems as well.
.
Therefore the above definition gives the generated language for these
systems as well.