


Next: Standard Watson-Crick E0L systems
Up: Watson-Crick systems
Previous: The main idea of
Contents
Standard Watson-Crick EDT0L systems
Now we present the construction by which we can give
for any recursively
enumerable language a generating standard Watson-Crick EDT0L system,
where the number of non-terminals
is bounded by a constant.
Theorem 6.4
Let
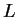
be a recursively enumerable language. Then there exists a
standard Watson-Crick
EDT0L system
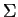
, such that
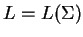
.
Moreover, the number of non-terminals of
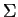
is bounded by a constant.
PROOF.
Let 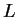 be a recursively enumerable language over an alphabet
be a recursively enumerable language over an alphabet
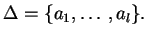 Then, according to
Theorem 6.3, there exists an EPC instance
Then, according to
Theorem 6.3, there exists an EPC instance
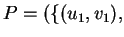
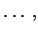
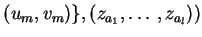 ,
where
,
where 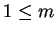 , and
, and
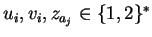 for
for
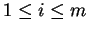 and
and
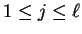 ,
such that
,
such that 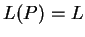 holds.
holds.
Now we define the simulating standard Watson-Crick EDT0L system
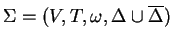 ,
and explain its functioning.
For the sake of readability, we use a notation for complementary
symbols slightly different
from the usual one:
the complementary symbol of
,
and explain its functioning.
For the sake of readability, we use a notation for complementary
symbols slightly different
from the usual one:
the complementary symbol of ![$ [X,i]$](img1232.gif) is
denoted by
is
denoted by
![$ [\ensuremath{{{\overline{X}}}},i].$](img1233.gif)
The alphabet 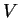 of the system
of the system 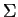 is the following:
is the following:
where
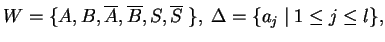 and
and 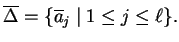 Symbols
Symbols 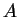 and
and 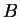 have the role explained in Section 6.2;
symbols
have the role explained in Section 6.2;
symbols 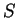 are used to start the derivation and to introduce the letters
are used to start the derivation and to introduce the letters
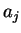 ; the barred letters, the pyrimidines,
play role only in the checking phase.
; the barred letters, the pyrimidines,
play role only in the checking phase.
The axiom is
![$ \omega=[S,0].$](img1238.gif)
The set of the tables is
There are two tables corresponding
to each pair 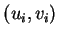 for
for
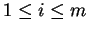 (
(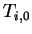 and
and 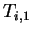 ), and there is a table corresponding to each
word
), and there is a table corresponding to each
word 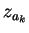 for
for
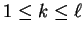 (
(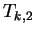 ).
Tables
).
Tables
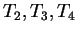 and
and 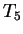 are used in switching from one phase
to another and in finishing the derivation
of the terminal words.
are used in switching from one phase
to another and in finishing the derivation
of the terminal words.
The tables contain the following rules and are used in the following way.
All the symbols which are not mentioned in a table are rewritten into 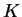 , these
rules make the tables complete. For
, these
rules make the tables complete. For
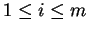 , let
, let
where
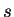 and
and 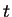 are the values of
are the values of 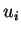 and
and 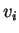 according to the base three
notation. (Actually,
according to the base three
notation. (Actually, 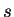 and
and 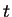 , as well as
, as well as 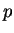 and
and 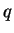 introduced
below, depend on
introduced
below, depend on 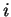 . We have disregarded the matter in our notation,
to improve readability.)
One of these tables is used to start the derivation and
to introduce
. We have disregarded the matter in our notation,
to improve readability.)
One of these tables is used to start the derivation and
to introduce 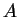 's and
's and 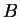 's into the sentential form according
to the corresponding pair
's into the sentential form according
to the corresponding pair 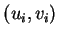 .
To start with, we have to use one of these tables
.
To start with, we have to use one of these tables 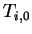 ,
thus it is ensured that at least
one pair
,
thus it is ensured that at least
one pair 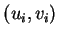 will be represented in the sentential form.
will be represented in the sentential form.
For
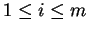 , let
, let
where
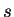 and
and 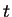 are the values, and
are the values, and
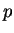 and
and 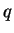 are the lengths of
are the lengths of 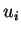 and
and 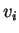 .
Using one of these tables, we can modify the
sentential form in such a way that it reflects the act of
concatenating the pair
.
Using one of these tables, we can modify the
sentential form in such a way that it reflects the act of
concatenating the pair
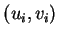 at the end of the pair of words
obtained so far.
By this concatenation, the values
at the end of the pair of words
obtained so far.
By this concatenation, the values 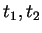 of the previously obtained
words become
of the previously obtained
words become
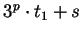 and
and
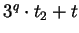 , respectively.
Using these tables several times,
by the end of the first phase of the derivation we obtain
a sentential form representing a pair
, respectively.
Using these tables several times,
by the end of the first phase of the derivation we obtain
a sentential form representing a pair
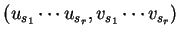 with
with 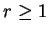 .
.
Let
This table switches a word with letters from ![$ [W,1]$](img1261.gif) to the corresponding
word with letters from
to the corresponding
word with letters from ![$ [W,2]$](img1262.gif) .
.
For
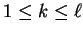 , let
, let
where
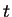 is the value and
is the value and 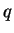 is the length of
is the length of 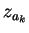 .
By these tables we can introduce letters
.
By these tables we can introduce letters 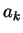 into the sentential form and
at the same time we can modify the sentential form in such a way that it
represents the act of
concatenating the pair
into the sentential form and
at the same time we can modify the sentential form in such a way that it
represents the act of
concatenating the pair
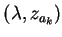 to a pair
to a pair
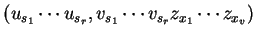 ,
,
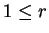 ,
, 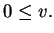 Hence by the end of the second phase we have
a sentential form representing
Hence by the end of the second phase we have
a sentential form representing
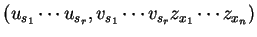 and the corresponding word
and the corresponding word
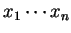 .
.
From now on, the derivation is done by table 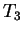 . This consists
of the following rules:
. This consists
of the following rules:
By this set of rules we check whether or not
the obtained sentential form 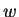 satisfies
satisfies
![$ {\vert w\vert}_{[A,3]}\geq {\vert w\vert}_{[\ensuremath{{{\overline{B}}}},3]}$](img1275.gif) .
If there are at least as many
.
If there are at least as many ![$ [A,3]$](img1276.gif) 's as
's as
![$ [\ensuremath{{{\overline{B}}}},3]$](img1277.gif) 's in
's in 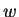 , then no
complementary transition takes place
and the derivation can go on. Otherwise in the next derivation step a
blocking situation occurs, the system will introduce symbols
, then no
complementary transition takes place
and the derivation can go on. Otherwise in the next derivation step a
blocking situation occurs, the system will introduce symbols 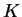 .
(We mentioned at the beginning of the proof, that all the letters not
mentioned here, including
.
(We mentioned at the beginning of the proof, that all the letters not
mentioned here, including
![$ [\ensuremath{{{\overline{A}}}},3]$](img1278.gif) and
and ![$ [B,3]$](img1279.gif) , are rewritten to
, are rewritten to 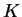 .)
.)
The next table is 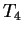 , with the rules
, with the rules
These rules are for checking whether or not the obtained sentential form
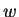 satisfies
satisfies
![$ {\vert w\vert}_{[\ensuremath{{{\overline{A}}}},4]}\leq {\vert w\vert}_{[B,4]}$](img1282.gif) .
We do it in the same way as we did in the previous
case:
if the sentential form goes through this checking as well,
that is, if no complementary transition takes place, then
the number of
.
We do it in the same way as we did in the previous
case:
if the sentential form goes through this checking as well,
that is, if no complementary transition takes place, then
the number of 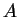 's and
's and 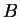 's are
equal in
's are
equal in 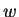 . Otherwise the system
blocks the derivation in the next step.
. Otherwise the system
blocks the derivation in the next step.
Then the application of table
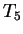 follows, with rules
follows, with rules
These rules finish the derivation by deleting all symbols not in  ,
therefore the derivation results in a word over
alph
,
therefore the derivation results in a word over
alph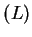 .
.
The construction of the standard Watson-Crick EDT0L system is based on the EPC
representing the recursively enumerable language 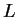 and
it is guaranteed that only those terminal words
and
it is guaranteed that only those terminal words
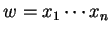 can be obtained by
can be obtained by 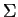 for which there exist some
pairs
for which there exist some
pairs
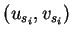 in the EPC, such that
in the EPC, such that
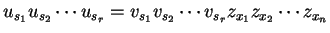 .
It is also clear that all these words can be derived, due to the working
of the construct presented above. Moreover, from the construction
we can also see that any terminal
word that can be generated by the system is over
.
It is also clear that all these words can be derived, due to the working
of the construct presented above. Moreover, from the construction
we can also see that any terminal
word that can be generated by the system is over 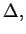 letters from
letters from
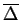 do not occur in a the generated
words.
Since these words are exactly
the words of
do not occur in a the generated
words.
Since these words are exactly
the words of 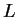 , we have proved that
, we have proved that
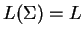 .
Moreover, we also can observe that the number of non-terminal letters is
bounded by a constant, namely 28. height 5pt width 5pt depth 0pt
.
Moreover, we also can observe that the number of non-terminal letters is
bounded by a constant, namely 28. height 5pt width 5pt depth 0pt
We note here that the only place where Watson-Crick complementarity is used
is the third phase, where we check the equality of letters 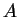 and
and 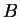 .
.



Next: Standard Watson-Crick E0L systems
Up: Watson-Crick systems
Previous: The main idea of
Contents
Csima Judit
2002-01-04
![]() ,
and explain its functioning.
For the sake of readability, we use a notation for complementary
symbols slightly different
from the usual one:
the complementary symbol of
,
and explain its functioning.
For the sake of readability, we use a notation for complementary
symbols slightly different
from the usual one:
the complementary symbol of ![]() is
denoted by
is
denoted by
![]()
![]() of the system
of the system ![]() is the following:
is the following:
![]()
![]() for
for
![]() (
(![]() and
and ![]() ), and there is a table corresponding to each
word
), and there is a table corresponding to each
word ![]() for
for
![]() (
(![]() ).
Tables
).
Tables
![]() and
and ![]() are used in switching from one phase
to another and in finishing the derivation
of the terminal words.
are used in switching from one phase
to another and in finishing the derivation
of the terminal words.
![]() , these
rules make the tables complete. For
, these
rules make the tables complete. For
![]() , let
, let
![]() , let
, let
![$\displaystyle T_{i,1}=\left\{[S,1]\ensuremath{\rightarrow}[S,1]{[A,1]}^s{[B,1]}...
...\rightarrow}{[A,1]}^{3^p}, [B,1]\ensuremath{\rightarrow}{[B,1]}^{3^q}\right\}
$](img1254.gif)
![]() , let
, let
![]() . This consists
of the following rules:
. This consists
of the following rules:
![]() , with the rules
, with the rules
![]() follows, with rules
follows, with rules
![]() ,
therefore the derivation results in a word over
alph
,
therefore the derivation results in a word over
alph![]() .
.
![]() and
it is guaranteed that only those terminal words
and
it is guaranteed that only those terminal words
![]() can be obtained by
can be obtained by ![]() for which there exist some
pairs
for which there exist some
pairs
![]() in the EPC, such that
in the EPC, such that
![]() .
It is also clear that all these words can be derived, due to the working
of the construct presented above. Moreover, from the construction
we can also see that any terminal
word that can be generated by the system is over
.
It is also clear that all these words can be derived, due to the working
of the construct presented above. Moreover, from the construction
we can also see that any terminal
word that can be generated by the system is over ![]() letters from
letters from
![]() do not occur in a the generated
words.
Since these words are exactly
the words of
do not occur in a the generated
words.
Since these words are exactly
the words of ![]() , we have proved that
, we have proved that
![]() .
Moreover, we also can observe that the number of non-terminal letters is
bounded by a constant, namely 28. height 5pt width 5pt depth 0pt
.
Moreover, we also can observe that the number of non-terminal letters is
bounded by a constant, namely 28. height 5pt width 5pt depth 0pt
![]() and
and ![]() .
.