Team behaviour in extended simple eco-grammar systems

In an extended simple eco-grammar system we distinguish a subset of the alphabet, and only words over this terminal alphabet are in the generated language.

The definition of the derivation mode $=k$ is the same as in Definition 3.1, the difference lies in the definition of the generated language.

Definition 3.4  
Consider an extended simple eco-grammar system $\Sigma=(\:V_E,P_E,R_1,\ldots,$ . The generated language in the derivation mode $=k$ is the following:

$$L(\Sigma,=k)=\{ v\in {\Delta}^* \vert\;{\omega}\ensuremath{\stackrel{=k} {{\Longrightarrow}_{\Sigma}^{*}}}v \}.$$

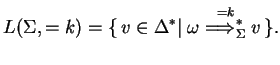
In this section we study extended simple eco-grammar systems with or without $\lambda$-rules. When we allow $\lambda$-rules in $P_E$ and in the sets $R_i$, we use the following notations: the class of languages generated by extended simple eco-grammar systems is denoted by ${\mathcal L}({EE}^{\lambda})$ (in this notation the first $E$ means ``extended'', the second one refers to ``eco''); the class of languages generated by systems containing $n$ agents and operating in the derivation mode $=k$ is denoted by ${\mathcal L}(EE^{\lambda}(n,=k))$. We omit the notation $\lambda$ if $\lambda$-rules are not allowed neither in $P_E$ nor in the sets $R_i$: ${\mathcal L}(EE)$ and ${\mathcal L}(EE(n,=k))$.

We present results about the hierarchy of language classes generated by $n$ agents in the derivation mode $=k$. Most of the statements and proofs are true with or without $\lambda$-rules, this fact is denoted by the superscript $(\lambda)$; sometimes a statement is true only when $\lambda$-rules are allowed, in this case we will emhasize this fact.

First we examine the role of the first parameter: the number of agents.

Lemma 3.5  
For $1\leq k\leq n\leq m$ ${{\mathcal L}(EE^{(\lambda)}(n,=k))}\subseteq {{\mathcal L}(EE^{(\lambda)}(m,=k))}$.

PROOF.
We show that for any $1\leq k\leq n\leq m$ and for any extended simple EG system $\ensuremath{\Sigma=(\:V_E,P_E,R_1,\ldots,} \ensuremath{R_n, \omega,\Delta\:)}$ there exists another extended simple EG system ${\ensuremath{{{\overline{\Sigma}}}}= (\:\ensuremath{{{\overline{V_E}}}},\ensur... ...}}}},\ensuremath{{{\overline{\omega}}}}, \ensuremath{{{\overline{\Delta}}}}\:)}$, such that their generated languages are equal, that is, $L({\Sigma},=k)=L(\ensuremath{{{\overline{\Sigma}}}},=k)$. Moreover, if $\Sigma$ does not contain $\lambda$-rules, then $\ensuremath{{{\overline{\Sigma}}}}$ is $\lambda$-free, too.
Let $\ensuremath{{{\overline{\Sigma}}}}$ be the following:

• $\ensuremath{{{\overline{V_E}}}}=V_E\cup \{K\}$, where $K\not \in V_E$,
• $\ensuremath{{{\overline{P_E}}}}=P_E\cup \{K\ensuremath{\rightarrow}K\}$,
• $\ensuremath{{{\overline{R_i}}}}=R_i$ for $1\leq i \leq n$,
• $\ensuremath{{{\overline{R_i}}}}=\{K\ensuremath{\rightarrow}K\}$ for $n+1\leq i\leq m$,
• $\ensuremath{{{\overline{\omega}}}}=\omega$, and
• $\ensuremath{{{\overline{\Delta}}}}=\Delta$.

It is clear that $L({\Sigma},=k)=L(\ensuremath{{{\overline{\Sigma}}}},=k)$ and $\ensuremath{{{\overline{\Sigma}}}}$ is $\lambda$-free if and only if $\Sigma$ does not contain $\lambda$-rules.height 5pt width 5pt depth 0pt

The following result shows that the above inclusion is not proper. The statement is true both with or without $\lambda$-rules.

Lemma 3.6  
For $1\leq k\leq n$ ${{\mathcal L}(EE^{(\lambda)}(n+1,=k))}\subseteq {{\mathcal L}(EE^{(\lambda)}(n,=k))}$.

PROOF.
Without $\lambda$-rules
We show that for any $\lambda$-free extended simple EG system ${R_{n+1}},{\omega},{\Delta}\:)$ working in the derivation mode $=k$ we can construct another $\lambda$-free extended simple EG system ${\ensuremath{{{\overline{\Sigma}}}}= (\:\ensuremath{{{\overline{V_E}}}},\ensur... ...}}}},\ensuremath{{{\overline{\omega}}}}, \ensuremath{{{\overline{\Delta}}}}\:)}$ working also in the derivation mode $=k$ simulating $\Sigma$.

Let $\ensuremath{{{\overline{\Sigma}}}}$ be the following system:

• $\ensuremath{{{\overline{V_E}}}}={V_E}^{}\cup {V_E}^{(2)}\cup {V_E}'\cup \{K\}$, where $K\not \in V_E$,
• $\ensuremath{{{\overline{P_E}}}}={P_E}^{\ensuremath{\rightarrow}(2)}\cup \{\;A... ...t\;A\in V_E\;\}\cup \{\;A'\ensuremath{\rightarrow}K\;\vert\;A\in V_E\;\}\;\cup$
  $\cup\;\{\;K\ensuremath{\rightarrow}K\;\}$, where ${P_E}^{\ensuremath{\rightarrow}(2)}= \{\;A^{}\ensuremath{\rightarrow}v^{(2)}\;\vert\; A\ensuremath{\rightarrow}v\in P_E\;\}$,

• $\ensuremath{{{\overline{R_1}}}}={{R_1}}^{\ensuremath{\rightarrow}(2)}\cup {{R'... ...ow}(2)}_{n+1}}\cup \{A'\ensuremath{\rightarrow}A^{}\;\vert\;A\in V_E\;\}\;\cup$
  $\cup \;\{{A}^{(2)}\ensuremath{\rightarrow}A^{}\;\vert\;A\in V_E\;\}$,
• $\ensuremath{{{\overline{R_i}}}}={{R_i}}^{\ensuremath{\rightarrow}(2)}\cup {{R'... ...(2)}_{n+1}}\cup \{{A}^{(2)}{\ensuremath{\rightarrow}A^{}}\;\vert\;A\in V_E\;\}$ for $2\leq i\leq n$, where ${{R_j}}^{\ensuremath{\rightarrow}(2)}= \{\;A^{}\ensuremath{\rightarrow}{{w}}^{(2)}\; \vert\; A\ensuremath{\rightarrow}w\in R_j\;\}$ for $1\leq j\leq n$, and
  ${{R'}^{\ensuremath{\rightarrow}(2)}_{n+1}}= \{\;A^{}\ensuremath{\rightarrow}{{w}'}^{(2)}\; \vert\; A\ensuremath{\rightarrow}w\in R_{n+1}\;\}$, where
  ${{w}'}^{(2)}=x_1^{(2)}\cdots x_{m-1}^{(2)}{x_m}'$ if $w=x_1\cdots x_{m-1}x_m$, $x_i\in V_E$, and $1\leq i\leq m$,
• $\ensuremath{{{\overline{\omega}}}}={\omega}^{}$, and
• $\ensuremath{{{\overline{\Delta}}}}={\Delta}^{}$.

The main idea of this construction is the following. We simulate one derivation step of $\Sigma$ by two corresponding derivation steps of $\ensuremath{{{\overline{\Sigma}}}}$. In the first simulation step we use the rules corresponding to the derivation step of $\Sigma$, the second step checks if the simulation is correct.

In $\ensuremath{{{\overline{\Sigma}}}}$, the set $R_{n+1}$ is included in the set of rules of each agent in the form of ${{{R'}}^{\ensuremath{\rightarrow}(2)}_{n+1}}$. When an agent uses a rule corresponding to $R_{n+1}$, a primed letter is introduced as well. The only agent which is able to make these primed letters disappear is $\ensuremath{{{\overline{R_1}}}}$; this construction guarantees (considering the rules of $\ensuremath{{{\overline{P_E}}}}$) that the derivation cannot terminate with a terminal word if the agents use more than one rule from ${R'}^{\ensuremath{\rightarrow}(2)}_{n+1}$ at the same derivation step.

If in a derivation step of $\Sigma$ the agents $R_{i_1},\ldots,R_{i_k}$ work and $i_j\leq n$ for $1\leq j\leq k$, then the simulation goes as follows.

In the first simulation step in $\ensuremath{{{\overline{\Sigma}}}}$ the agents $\ensuremath{{{\overline{R_{i_1}}}}},\ldots,\ensuremath{{{\overline{R_{i_k}}}}}$ work using rules from ${{R_{i_j}}^{\ensuremath{\rightarrow}(2)}}$, corresponding to the step of $\Sigma$. Then the environment uses the same rules as in $\Sigma$ (in the form of ${P_E}^{\ensuremath{\rightarrow}(2)}$).

In the second simulation step the agents $\ensuremath{{{\overline{R_{i_1}}}}},\ldots,\ensuremath{{{\overline{R_{i_k}}}}}$ rewrite $k$ letters and the environment rewrites the remaining letters by using the rules in the form of $A^{(2)}\ensuremath{\rightarrow}A^{}$. (There are at least $k$ letters in the sentential form because there are no $\lambda$-rules in $\Sigma$.)

If $R_{n+1}$ was among the agents $R_{i_1},\ldots ,R_{i_{k-1}},R_{i_k}=R_{n+1}$ in a derivation step in $\Sigma$, then the two simulation steps of $\ensuremath{{{\overline{\Sigma}}}}$ are the following.

In the first simulation step we choose one agent $\ensuremath{{{\overline{R_s}}}}$ in $\ensuremath{{{\overline{\Sigma}}}}$, such that $s\not =i_j$ for any $1\leq j\leq k-1$. This is possible because $k\leq n$. This agent simulates the work of $R_{n+1}$ by using the corresponding rule of ${R'}^{\ensuremath{\rightarrow}(2)}_{n+1}$.

The agents $\ensuremath{{{\overline{R_{i_1}}}}},\ldots ,\ensuremath{{{\overline{{R}_{i_{k-1}}}}}}$ simulate the other rules of the agents and the environment rewrites the remaining letters in the same way as in $\Sigma$.

In the second simulation step $\ensuremath{{{\overline{R_1}}}}$ rewrites the primed letter, other $k-1$ agents rewrite $k-1$ other letters and the environment rewrites the remaining letters into symbols of ${V_E}^{}$.

Since we can simulate every derivation step of $\Sigma$ by a derivation sequence of $\ensuremath{{{\overline{\Sigma}}}}$, we obtain $L(\Sigma,=k)\subseteq L(\ensuremath{{{\overline{\Sigma}}}},=k)$.

On the other hand, for any derivation sequence of $\ensuremath{{{\overline{\Sigma}}}}$ resulting in a terminal word, there exists a derivation in $\Sigma$ generating the same word, which gives the other inclusion $L(\ensuremath{{{\overline{\Sigma}}}},=k)\subseteq L({\Sigma},=k)$. We will simulate two derivation steps of these sequences of $\ensuremath{{{\overline{\Sigma}}}}$ by one step of $\Sigma$. For each $v\in L(\ensuremath{{{\overline{\Sigma}}}},=k)$ (which implies $v\in {{\Delta}^{}}^+$ because $\lambda$-rules are not allowed) there exists a derivation sequence in $\ensuremath{{{\overline{\Sigma}}}}$ in the form of

$$\ensuremath{{{\overline{\omega}}}}\ensuremath{{\Rightarrow}_{\ens... ...}}}\cdots \ensuremath{{\Rightarrow}_{\ensuremath{{{\overline{\Sigma}}}}}}v_t=v.$$

Since $v\in {{V_E}^{}}^+$, there are neither primed letters nor letters $K$ in $v$.

Considering the rules in $\ensuremath{{{\overline{P_E}}}}$, it is easy to see that there can be at most one primed letter in the previous word $v_{t-1}$.

The fact that there is no primed letter in $v_{t-1}$ means that in the $(t-1)$th step $k$ agents, $\ensuremath{{{\overline{R_{i_1}}}}},\ldots,\ensuremath{{{\overline{R_{i_k}}}}}$, use rules from the sets ${R_{i_j}}^{{}\ensuremath{\rightarrow}{(2)}}$ with $1\leq i_j\leq n$. In this case we can simulate the last two derivation steps of $\ensuremath{{{\overline{\Sigma}}}}$ by one derivation step of $\Sigma$, using the corresponding rules of the agents ${R_{i_1}},\ldots, {R_{i_k}}$ and the environment.

The other possibility gives that $k-1$ agents, $\ensuremath{{{\overline{R_{i_1}}}}},\ldots ,\ensuremath{{{\overline{{R}_{i_{k-1}}}}}}$, use rules from the sets ${{R_{i_j}}}^{\ensuremath{\rightarrow}(2)}$ with $1\leq i_j\leq n$ and one agent uses a rule of ${{R'}^{\ensuremath{\rightarrow}(2)}_{n+1}}$. Then we can simulate the last two steps by one step in $\Sigma$ when the agents $R_{i_1},\ldots ,R_{i_{k-1}},R_{n+1}$ and the environment use the corresponding rules.

In both cases $v_{t-2}\in {{V_E}^{}}^+$, thus we can continue the simulation by giving the role of $v$ to $v_{t-2}$. Since the axiom is over ${V_E}^{}$ and $t$ is an even number (see the rules of $\ensuremath{{{\overline{\Sigma}}}}$), it can be proved by induction on the length of the derivation that we can simulate the whole derivation sequence.

With $\lambda$-rules
The main idea is the same as it was in the $\lambda$-free case: we show that we can simulate any extended simple EG system $\ensuremath{{\Sigma}= (\:{V_E},{P_E},{R_1},\ldots,} \ensuremath{{R_{n+1}},{\omega},{\Delta}\:)}$ working in the derivation mode $=k$ by another extended simple EG system ${\ensuremath{{{\overline{\Sigma}}}}= (\:\ensuremath{{{\overline{V_E}}}},\ensur... ...}}}},\ensuremath{{{\overline{\omega}}}}, \ensuremath{{{\overline{\Delta}}}}\:)}$ working also in the derivation mode $=k$.

Let $\ensuremath{{{\overline{\Sigma}}}}$ be the following system:

• $\ensuremath{{{\overline{V_E}}}}={V_E}^{}\cup {V_E}^{(2)}\cup \{K,T_1,T_2\}$, where $K,T_1,T_2 \not \in V_E$,
• $\ensuremath{{{\overline{P_E}}}}={P_E}^{\ensuremath{\rightarrow}(2)}\cup \{\;A^{(2)}\ensuremath{\rightarrow}A^{}\;\vert\;A\in V_E\;\}\cup$
  $\{\;K\ensuremath{\rightarrow}K,T_1\ensuremath{\rightarrow}K,T_2\ensuremath{\rightarrow}\lambda\;\}$,
• $\ensuremath{{{\overline{R_1}}}}={{R_1}}^{\ensuremath{\rightarrow}(2)}T_2\cup {... ...suremath{\rightarrow}\lambda\;\}\cup \{\;T_2\ensuremath{\rightarrow}\lambda\;\}$,
• $\ensuremath{{{\overline{R_i}}}}={{R_i}}^{\ensuremath{\rightarrow}(2)}T_2\cup {... ...emath{\rightarrow}(2)}_{n+1}T_1\cup \{\;T_2\ensuremath{\rightarrow}\lambda\;\}$ for $2\leq i\leq n$,
  where
  ${{R_j}}^{\ensuremath{\rightarrow}(2)}T_2= \{\;A^{}\ensuremath{\rightarrow}{{w}}^{(2)}T_2\; \vert\; A\ensuremath{\rightarrow}w\in R_j\;\}$ for $1\leq j\leq n$ and
  ${R^{\ensuremath{\rightarrow}(2)}_{n+1}}T_1= \{\;A^{}\ensuremath{\rightarrow}{{w}}^{(2)}T_1\; \vert\; A\ensuremath{\rightarrow}w\in R_{n+1}\;\}$,
• $\ensuremath{{{\overline{\omega}}}}={\omega}^{}$, and
• $\ensuremath{{{\overline{\Delta}}}}={\Delta}^{}$.

The statement $L(\Sigma,=k)=L(\ensuremath{{{\overline{\Sigma}}}},=k)$ can be proved similarly to the $\lambda$-free case: $T_1$ plays the role of the primed letters, it controls the usage of the rules of ${R}^{\ensuremath{\rightarrow}(2)}_{n+1}$; $T_2$ letters guarantee that $k$ agents could work in the second simulation step even if in the first simulation step $\lambda$-rules were applied.height 5pt width 5pt depth 0pt

From the two previous lemmas we obtain the following corollary, which says that the first parameter has no influence on the class of generated languages.

Corollary 3.7  
For $1\leq k\leq n$ ${{\mathcal L}(EE^{(\lambda)}(n,=k))}= {{\mathcal L}(EE^{(\lambda)}(k,=k))}$.

Now we turn our attention to the second parameter: the number of agents working in a derivation step. Considering Corollary 3.7, it is enough to examine the relations of language classes ${{\mathcal L}(EE^{(\lambda)}(k,=k))}$.

For the $\lambda$-free case, it was proved in [Dassow and MihalacheDassow and Mihalache1995] that ${{\mathcal L}(EE^{}(n+1,=n+1))}$ is included in ${{\mathcal L}(EE^{}(n,=n))}$. In the following lemma we present the same result for extended simple EG systems with $\lambda$-rules as well. We give a simulation which is based on the construction used in [Dassow and MihalacheDassow and Mihalache1995], hence in the first part of our proof we briefly summarise their construction and their explanation for the $\lambda$-free case. Then in the second part of the proof we give the modifications which are necessary to obtain the same result when $\lambda$-rules are allowed.

Lemma 3.8  
For $1\leq n$ ${{\mathcal L}(EE^{(\lambda)}(n+1,=n+1))}\subseteq {{\mathcal L}(EE^{(\lambda)}(n,=n))}$.

PROOF.
The $\lambda$-free case (from [Dassow and MihalacheDassow and Mihalache1995]):

For any extended simple EG system $\ensuremath{{\Sigma}= (\:{V_E},{P_E},{R_1},\ldots,} \ensuremath{{R_{n+1}},{\omega},{\Delta}\:)}$ we give another extended simple EG system $\ensuremath{{{\overline{\Sigma}}}}=(\ensuremath{{{\overline{V_E}}}}, \ensurema... ...1}}}}}, \ensuremath{{{\overline{\omega}}}}, \ensuremath{{{\overline{\Delta}}}})$, such that $L(\Sigma, =n+1)=L(\ensuremath{{{\overline{\Sigma}}}},=n)$.

Let $\ensuremath{{{\overline{\Sigma}}}}$ be the following:

• $\ensuremath{{{\overline{V_E}}}}={V_E}\cup {V_E}'\cup \{\bar{A}\;\vert \;A\ensuremath{\rightarrow}\alpha\in R_{n+1}\}\cup \{K\}$, where $K\not \in V_E$,
• $\ensuremath{{{\overline{P_E}}}}=\{\;A\ensuremath{\rightarrow}{\alpha}'\;\vert\... ...ightarrow}\bar{A}\;\vert\;A\ensuremath{\rightarrow}\alpha \in R_{n+1}\;\}\;\cup$
  $\cup\; \{\;A'\ensuremath{\rightarrow}A\;\vert\;A\in V_E\;\}\cup \{\;\bar{A}\e... ...emath{\rightarrow}\alpha \in R_{n+1}\;\} \cup\{\;K\ensuremath{\rightarrow}K\;\}$,
• $\ensuremath{{{\overline{R_1}}}}=\{A\ensuremath{\rightarrow}{\alpha}'\;\vert\;A... ...th{\rightarrow}{\alpha}\;\vert\;A\ensuremath{\rightarrow}\alpha \in R_{n+1}\;\}$,
• $\ensuremath{{{\overline{R_i}}}}=\{A\ensuremath{\rightarrow}{\alpha}'\;\vert\;A... ...ow}\alpha\in R_i\;\}\cup \{{A}'\ensuremath{\rightarrow}{A}\;\vert\;A\in V_E\;\}$ for $2\leq i\leq n$,
• $\ensuremath{{{\overline{\omega}}}}={\omega}$, and
• $\ensuremath{{{\overline{\Delta}}}}={\Delta}$.

Let

$$x=x_1Z_1x_2Z_2\cdots x_{n+1}Z_{n+1}x_{n+2}\ensuremath{{\Rightarrow}_{}}y_1w_1y_2w_2\cdots y_{n+1}w_{n+1}y_{n+2}=y$$

be a derivation step in $\Sigma$, where the rules used by the agents are $Z_i\ensuremath{\rightarrow}w_i$ for $1\leq i\leq n+1$ and the derivations $x_j\ensuremath{{\Rightarrow}_{}} y_j$ for $1\leq j\leq n+2$ are performed by the environment. We can simulate this step by two steps of $\ensuremath{{{\overline{\Sigma}}}}$ in the following way. (We suppose that $R_{n+1}$ used the rule $Z_{n+1}\ensuremath{\rightarrow}w_{n+1}$.)

$$x=x_1Z_1x_2Z_2\cdots x_{n+1}Z_{n+1}x_{n+2}\ensuremath{{\Rightarro... ...}'\cdots {y'_{n+1}} {\overline{Z}_{n+1}}{y'_{n+2}}\ensuremath{{\Rightarrow}_{}}$$

$$\ensuremath{{\Rightarrow}_{}}y_1w_1y_2w_2\cdots y_{n+1}w_{n+1}y_{n+2}=y$$

It follows from the construction that the environment cannot introduce two barred letters, because in this case the derivation would never result in a terminal word because of the symbol $K$. Therefore, only the sequences consisting of pairs of steps of this type can derive terminal words in $\ensuremath{{{\overline{\Sigma}}}}$, but these derivations can be performed in $\Sigma$ as well.

In the case when $\lambda$-rules are allowed we have to modify the above construction in the following way.

• $\ensuremath{{{\overline{V_E}}}}={V_E}\cup {V_E}'\cup \{\bar{A}\;\vert\;A\ensuremath{\rightarrow}\alpha \in R_{n+1}\}\cup \{K,\;Z\}$, where $K,\;Z\not \in V_E$,
• $\ensuremath{{{\overline{P_E}}}}=\{\;A\ensuremath{\rightarrow}{\alpha}'\;\vert\... ...\rightarrow}\bar{A}\;\vert\;A\ensuremath{\rightarrow}\alpha \in R_{n+1}\;\}\cup$
  $\cup \{\;A'\ensuremath{\rightarrow}A\;\vert\;A\in V_E\;\}\cup \{\;\bar{A}\ensuremath{\rightarrow}K\;\vert\;A\ensuremath{\rightarrow}\alpha \in R_{n+1}\;\}\cup$
  $\cup\{\;K\ensuremath{\rightarrow}K\;\}\cup\{\;Z\ensuremath{\rightarrow}\lambda\;\}$,
• $\ensuremath{{{\overline{R_1}}}}=\{A\ensuremath{\rightarrow}{\alpha}'Z\;\vert\;... ...th{\rightarrow}{\alpha}\;\vert\;A\ensuremath{\rightarrow}\alpha \in R_{n+1}\;\}$,
• $\ensuremath{{{\overline{R_i}}}}=\{A\ensuremath{\rightarrow}{\alpha}'Z\;\vert\;... ...remath{\rightarrow}\alpha\in R_i\;\}\cup \{Z\ensuremath{\rightarrow}\lambda\;\}$ for $2\leq i\leq n$,
• $\ensuremath{{{\overline{\omega}}}}={\omega}$, and
• $\ensuremath{{{\overline{\Delta}}}}={\Delta}$.

Here the letters $Z$ guarantee that the agents can apply a rule in $\ensuremath{{{\overline{\Sigma}}}}$ in the second simulation step, even if in the first step $\lambda$-rules were used. Besides this modification, the construction is the same as in the $\lambda$-free case. Thus, we have $L(\Sigma, =n+1)=L(\ensuremath{{{\overline{\Sigma}}}},=n)$ by the same reason as in the $\lambda$-free case.height 5pt width 5pt depth 0pt

There remains only one relation to examine: whether the language classes ${{\mathcal L}(EE^{(\lambda)}(n,=n))}$ are included in ${{\mathcal L}(EE^{(\lambda)}(n+1,=n+1))}$ or the inclusion in Lemma 3.8 is strict. The answer depends on $\lambda$-rules. When $\lambda$-rules are allowed, the two language classes are equal.

Lemma 3.9  
For $1\leq n$ ${{\mathcal L}(EE^{\lambda}(n,=n))}\subseteq {{\mathcal L}(EE^{\lambda}(n+1,=n+1))}$.

PROOF.
For any extended simple EG system $\ensuremath{\Sigma=(\:V_E,P_E,R_1,\ldots,} \ensuremath{R_n, \omega,\Delta\:)}$ we give another extended simple EG system ${\ensuremath{{{\overline{\Sigma}}}}= (\:\ensuremath{{{\overline{V_E}}}},\ensur... ...}}}},\ensuremath{{{\overline{\omega}}}}, \ensuremath{{{\overline{\Delta}}}}\:)}$ containing $\lambda$-rules, such that $L(\Sigma, =n)=L(\ensuremath{{{\overline{\Sigma}}}},=n+1)$.
Let $\ensuremath{{{\overline{\Sigma}}}}$ be the following:

• $\ensuremath{{{\overline{V_E}}}}=V_E\cup \{K\}$, where $K\not \in V_E$,
• $\ensuremath{{{\overline{P_E}}}}=P_E\cup \{K\ensuremath{\rightarrow}K\}$,
• $\ensuremath{{{\overline{R_i}}}}=R_i$ for $1\leq i \leq n$,
• $\ensuremath{{{\overline{R_{n+1}}}}}=\{K\ensuremath{\rightarrow}K,K\ensuremath{\rightarrow}\lambda\}$,
• $\ensuremath{{{\overline{\omega}}}}=\omega K$, and
• $\ensuremath{{{\overline{\Delta}}}}=\Delta$.

For any $v\in L(\Sigma, =n)$ there is a derivation in $\Sigma$ in the form of

$$\omega\ensuremath{{\Rightarrow}_{}}v_1\ensuremath{{\Rightarrow}_{}}\cdots\ensuremath{{\Rightarrow}_{}}v_t=v$$

where in the $i$th step ( $1\leq i\leq t$) the agents $R_j$ use the rules ${r_j}_i$. Let us consider the following derivation in $\ensuremath{{{\overline{\Sigma}}}}$

$$\omega K \ensuremath{{\Rightarrow}_{}}v_1K \ensuremath{{\Rightarr... ...}}\cdots\ensuremath{{\Rightarrow}_{}}v_{t-1}K\ensuremath{{\Rightarrow}_{}}v_t=v$$

where in the $i$th step ( $1\leq i\leq t-1$) the agents $\ensuremath{{{\overline{R_j}}}}$ ( $1\leq j\leq n$) apply the rules ${r_j}_i$ corresponding to the above derivation and the agent $\ensuremath{{{\overline{R_{n+1}}}}}$ uses the rule $K\ensuremath{\rightarrow}K$; in the last step the agents $\ensuremath{{{\overline{R_j}}}}$ use the corresponding rules ${r_j}_t$ (for $1\leq j\leq n$) and $\ensuremath{{{\overline{R_{n+1}}}}}$ uses the rule $K\ensuremath{\rightarrow}\lambda$. In this way we can simulate $\Sigma$ by $\ensuremath{{{\overline{\Sigma}}}}$.

Now we show that $L(\ensuremath{{{\overline{\Sigma}}}}, =n+1) \subseteq L({\Sigma},=n)$. For any $v\in L(\ensuremath{{{\overline{\Sigma}}}},=n+1)$ there is a derivation in $\ensuremath{{{\overline{\Sigma}}}}$ in the form

$$\ensuremath{{{\overline{\omega}}}}=\omega K \ensuremath{{\Rightar... ...{}}\cdots\ensuremath{{\Rightarrow}_{}}v_{t-1}\ensuremath{{\Rightarrow}_{}}v_t=v$$

where in each derivation step all the $n+1$ agents work. Since $v$ is over $\ensuremath{{{\overline{\Delta}}}}={\Delta}$, there are no letters $K$ in it. But in the last step $n+1$ agents must work and the last agent can use only the rules $K\ensuremath{\rightarrow}K$ or $K\ensuremath{\rightarrow}\lambda$. Moreover, considering that $\ensuremath{{{\overline{\omega}}}}$ contains one $K$ and that there is no rule producing new letters $K$, we get that all words in the above derivation, except $v$, contain exactly one letter $K$. We also get that in the first $t-1$ step the $(n+1)$th agent has to use the rule $K\ensuremath{\rightarrow}K$ and it has to use the rule $K\ensuremath{\rightarrow}\lambda$ in the last step. But in this case we can simulate this derivation of $\ensuremath{{{\overline{\Sigma}}}}$ by the following derivation in $\Sigma$:

$$\omega=f(\ensuremath{{{\overline{\omega}}}})\ensuremath{{\Rightar... ...ensuremath{{\Rightarrow}_{}}f(v_{t-1})\ensuremath{{\Rightarrow}_{}}f(v_t)=v_t=v$$

where $f$ is a homomorphism over $V_E\cup\{K\}$ defined as follows:

$$f(z) = \left \{ \begin{array}{ll} z & \mbox{if $z\in V_E$} \\ \lambda & \mbox{if $z=K$} \end{array}\right.$$

In the above derivation the agents $R_1,R_2,\ldots, R_n$ use the rules corresponding to the derivation of $\ensuremath{{{\overline{\Sigma}}}}$.height 5pt width 5pt depth 0pt

On the other hand, in the $\lambda$-free case the inclusion is proper between the language classes ${{\mathcal L}(EE^{}(n,=n))}$ and ${{\mathcal L}(EE^{}(n+1,=n+1))}$.

Lemma 3.10  
For any $1\leq n$ there exists a language $L$, such that

$$L\in {{\mathcal L}(EE^{}(n,=n))}\setminus {{\mathcal L}(EE^{}(n+1,=n+1))}.$$

PROOF.
Let $L$ be the finite language $\{\;a^{n},b^{n}\;\}$. It is clear that it can be generated by an extended simple EG system working in the derivation mode $=n$. Moreover, it cannot be generated by using the derivation mode $=\ell$ if $\ell>n$ because in this case either the letters in the axiom are not enough to perform an action of $\ell$ agents or we should use $\lambda$-rules which is not allowed.height 5pt width 5pt depth 0pt

Concluding our investigations, from Corollary 3.7, Lemma 3.8 and Lemma 3.9 we obtain the following theorem. It says that when $\lambda$-rules are allowed, neither the number of the agents being in the system nor the number of the agents working in a derivation step have any influence on the generated languages.

Theorem 3.11  
For $1\leq k\leq n$ ${{\mathcal L}(EE^{\lambda}(n,=k))}={{\mathcal L}(EE^{\lambda}(1,=1))}$.

In the $\lambda$-free case we use the notation ${\mathcal L}(EE(=k))$ for the class of languages which can be generated by extended simple EG systems working in the derivation mode $=k$, without $\lambda$-rules. From Corollary 3.7 we have $\;{{\mathcal L}(EE^{}(n,=k))}={\mathcal L}(EE(=k))$ for $1\leq k\leq n$.

Using this fact together with Lemma 3.8 and Lemma 3.10, we can present the result of the $\lambda$-free case in the following theorem.

Theorem 3.12  
${\mathcal L}(EE(=1)) \supset {\mathcal L}(EE(=2))\supset \cdots \supset {\mathcal L}(EE(=k))\supset \cdots \;\;\;$ for $1\leq i$.

We summarise the results of this section in the form of a diagram, where a straight arrow indicates a proper inclusion; the class the arrow leaves is included in the class the arrow points at. The inclusion ${{\mathcal L}(EE^{}(1,=1))} \subset {{\mathcal L}(EE^{\lambda}(1,=1))}$ can be proved by any language of ${{\mathcal L}(EE^{\lambda}(1,=1))}$ containing the empty word, $\lambda$.

We use the notation $n_i$ for $1\leq i$, where $n_i$ denotes an arbitrary positive integer, such that $i\leq n_i$.

Figure 3.1: Hierarchy in team derivation mode