- Van-e
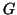 -ben Euler-kör vagy Euler-út?
-ben Euler-kör vagy Euler-út?
- Van-e
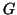 -ben Hamilton-kör vagy Hamilton-út?
-ben Hamilton-kör vagy Hamilton-út?
Megoldás:
- A
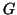 gráf összefüggő, így Euler-kör illetve -út
létezésének eldöntéséhez
gráf összefüggő, így Euler-kör illetve -út
létezésének eldöntéséhez 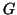 fokszámait kell megvizsgálnunk. A
feltételek szerint
fokszámait kell megvizsgálnunk. A
feltételek szerint 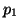 és
és 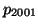 fokszáma 2,
fokszáma 2, 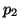 és
és
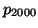 fokszáma 3, végezetül
fokszáma 3, végezetül
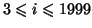 esetén
esetén 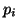 fokszáma 4.
fokszáma 4.
Összességében tehát megállapítható, hogy
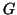 -nek pontosan két
páratlan fokszámú csúcsa van, ezért Euler-utat tartalmaz, de
Euler-kört nem.
-nek pontosan két
páratlan fokszámú csúcsa van, ezért Euler-utat tartalmaz, de
Euler-kört nem.
- A legegyszerűbb Hamilton-út a csúcsok növekvő index szerinti
bejárásával kapható, hiszen
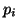 és
és 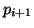 minden
minden
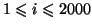 esetén szomszédosak. Sajnos ez a
Hamilton-út nem terjeszthető ki egyetlen él behúzásával
Hamiton-körré.
esetén szomszédosak. Sajnos ez a
Hamilton-út nem terjeszthető ki egyetlen él behúzásával
Hamiton-körré.
Könnyű ellenőrizni azonban, hogy a csúcsok következő sorrendben való bejárása Hamilton-kört ad:
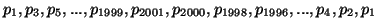 .
Természetesen ennek egy élét elhagyva szintén Hamilton-utat
kapunk.
.
Természetesen ennek egy élét elhagyva szintén Hamilton-utat
kapunk.
Megoldás:
Azonos paritású számok között biztosan nem megy él, hiszen az ilyen számpárok összege páros, ami nem lehet relatív prím 74-hez. Bizonyos számpárok összege lehet továbbá 37, 74 vagy 111, mely esetekben az adott számpár szintén nincs összekötve. Minden egyéb számpár össze van kötve.
Ennek alapján ![]() egy jó színezését kapjuk, ha a páros számokat
pirosra, a páratlanokat pedig kékre festjük.
egy jó színezését kapjuk, ha a páros számokat
pirosra, a páratlanokat pedig kékre festjük. ![]() tartalmaz élet, így
egyetlen színnel biztosan nem színezhető. Ezek alapján
tartalmaz élet, így
egyetlen színnel biztosan nem színezhető. Ezek alapján ![]() .
.
Vizsgáljuk a lefogó élek minimális számát (![]() ). Egyfelől ez a
szám nyilván legalább 37, hisz egy él legfeljebb két pontot foghat
le. Másfelől megadható 37 él, melyek
). Egyfelől ez a
szám nyilván legalább 37, hisz egy él legfeljebb két pontot foghat
le. Másfelől megadható 37 él, melyek ![]() összes pontját lefogják,
éspedig az
összes pontját lefogják,
éspedig az
![]() élek. Ezen élek
csúcsaihoz tartozó számok összege ugyanis minden esetben 75, ami
relatív prím 74-hez, tehát ezek valóban
élek. Ezen élek
csúcsaihoz tartozó számok összege ugyanis minden esetben 75, ami
relatív prím 74-hez, tehát ezek valóban ![]() élei. Ezért
élei. Ezért
![]() .
.
A ![]() gráf hurokmentes, ezért alkalmazható Gallai tétele, amely
szerint
gráf hurokmentes, ezért alkalmazható Gallai tétele, amely
szerint
![]() , ennek alapján
, ennek alapján ![]() .
.
A ![]() gráf páros és nem tartalmaz izolált pontot, így König
tételének mindkét állítása alkalmazható, amely szerint
gráf páros és nem tartalmaz izolált pontot, így König
tételének mindkét állítása alkalmazható, amely szerint
![]() és
és
![]() . Tehát a lefogó pontok
minimális száma
. Tehát a lefogó pontok
minimális száma ![]() , a független pontok maximális száma
pedig
, a független pontok maximális száma
pedig ![]() .
.
Megoldás:
Legyen a ![]() -ből elhagyott él
-ből elhagyott él ![]() . Indirekt módon tegyük fel,
hogy az állítás nem igaz. Ekkor a
. Indirekt módon tegyük fel,
hogy az állítás nem igaz. Ekkor a ![]() gráfból elhagyható
legfeljebb
gráfból elhagyható
legfeljebb ![]() pont úgy, hogy ne maradjon összefüggő.
Tekintsük ugyanezen legfeljebb
pont úgy, hogy ne maradjon összefüggő.
Tekintsük ugyanezen legfeljebb ![]() pontot
pontot ![]() -ben. Ha
-ben. Ha ![]() egyik végpontja sincs köztük, akkor vegyük hozzájuk a kettő
közül pontosan az egyiket. Így legfeljebb
egyik végpontja sincs köztük, akkor vegyük hozzájuk a kettő
közül pontosan az egyiket. Így legfeljebb ![]() pontot kaptunk,
melyeket
pontot kaptunk,
melyeket ![]() -ből elhagyva az nem marad összefüggő. Ez azonban
ellentmond annak, hogy
-ből elhagyva az nem marad összefüggő. Ez azonban
ellentmond annak, hogy ![]() eredetileg
eredetileg ![]() -szorosan
pontösszefüggő volt.
-szorosan
pontösszefüggő volt.
Megoldás:
Könnyű ellenőrizni, hogy bármely páratlan szám négyzete 1-et ad
8-cal osztva maradékul (
![]() ).
).
Indirekt módon tegyük fel, hogy ![]() nem osztható néggyel, ekkor
alkalmas
nem osztható néggyel, ekkor
alkalmas ![]() egész szám választása esetén
egész szám választása esetén ![]() . Ekkor
. Ekkor
![]() . Ekkor azonban
. Ekkor azonban
![]() ellentmond a fenti megállapításunknak, ez az
ellentmondás bizonyítja a feladat állítását.
ellentmond a fenti megállapításunknak, ez az
ellentmondás bizonyítja a feladat állítását.
Megoldás:
![]() , ezért a kongruenciának pontosan három megoldása
lesz modulo 12, vagy másképpen mondva pontosan egy megoldása lesz
modulo 4. A 3-mal való osztás elvégzése után
, ezért a kongruenciának pontosan három megoldása
lesz modulo 12, vagy másképpen mondva pontosan egy megoldása lesz
modulo 4. A 3-mal való osztás elvégzése után
![]() , azaz
, azaz
![]() adódik. Mindkét oldalt 3-mal
szorozva (figyelem! itt változatlan marad a modulus) kapjuk a
megoldást:
adódik. Mindkét oldalt 3-mal
szorozva (figyelem! itt változatlan marad a modulus) kapjuk a
megoldást:
![]() .
.
Megoldás:
A faktorcsoport elemszáma:
![]() , ami
prímszám. Ismeretes, hogy minden prímrendű csoport ciklikus. A
, ami
prímszám. Ismeretes, hogy minden prímrendű csoport ciklikus. A
![]() faktorcsoport tehát ciklikus, ezért kommutatív.
faktorcsoport tehát ciklikus, ezért kommutatív.