Bevezetés a számításelméletbe
1. zárthelyi, 2001. október 31.

  1. Adjuk meg az alábbi egyenletekkel megadott $S_1, S_2$ és $S_3$ síkok összes metszéspontját a háromdimenziós valós térben.


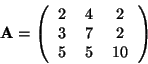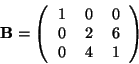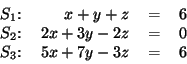
    \begin{displaymath} \begin{tabular}{rrcl} $S_1$: & $x+y+z$\ & = & 6\\ $S_2$:... ...y-2z$\ & = & 0\\ $S_3$: & $5x+7y-3z$\ & = & 6 \end{tabular} \end{displaymath}

    Megoldás:

    A kérdezett közös pontok a fenti három egyenletből álló egyenletrendszer megoldását adó $(x,y,z)$ valós számhármasokkal, mint koordinátákkal megadható pontok.

    A Gauss-eliminációs eljárással a következő mátrixokhoz jutunk:


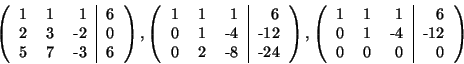
    \begin{displaymath} \left( \begin{tabular}{rrr} 1 & 1 & 1 \\ 2 & 3 & -2 \\ ... ... \begin{tabular}{r} 6 \\ -12 \\ 0 \end{tabular} \right) \end{displaymath}

    amiből a redukált lépcsős alak azonnal adódik:


    \begin{displaymath} \left( \begin{tabular}{ccc} 1 & 0 & 5 \\ 0 & 1 & -4 \e... ...vline \begin{tabular}{c} 18 \\ -12 \end{tabular} \right) \end{displaymath}

    Innen a megoldás leolvasható: $x=18-5z, y=-12+4z,$ miközben $z$ tetszőlegesen megválasztható valós szám.

  2. Igaz-e, hogy minden véges dimenziós vektortérnek véges sok altere van?

    Megoldás:

    Nem igaz, megadunk egy ellenpéldát: a háromdimenziós valós térnek például minden ezen térben elhelyezkedő, az origón áthaladó sík altere, ilyen pedig végtelen sok van, miközben a tér dimenziója véges.

  3. Legyenek $S_1$ és $S_2$ az $n$-dimenziós valós tér olyan alterei, melyekre $\forall \textbf{x} \in S_1$ és $\forall \textbf{y} \in S_2$ vektorok esetén teljesül, hogy $\textbf{x}$ és $\textbf{y}$ lineárisan független (feltételezve, hogy egyikük sem egyenlő a $\textbf{0}$ vektorral).

    Legyenek $\textbf{x}^{(1)}, \textbf{x}^{(2)}, \ldots, \textbf{x}^{(k)} \in S_1$ lineárisan független vektorok, és $\textbf{y}^{(1)}, \textbf{y}^{(2)}, \ldots, \textbf{y}^{(m)} \in S_2$ szintén lineárisan független vektorok. Bizonyítsuk be, hogy ekkor az $\textbf{x}^{(1)}, \textbf{x}^{(2)}, \ldots, \textbf{x}^{(k)}, \textbf{y}^{(1)}, \textbf{y}^{(2)}, \ldots, \textbf{y}^{(m)}$ vektorokból álló (összesen tehát $(k+m)$ vektort tartalmazó) vektorrendszer is lineárisan független.

    Megoldás:

    Indirekt módon tegyük fel, hogy nem igaz az állítás, ekkor léteznek olyan $\lambda_i$ és $\mu_j$ $(1 \leqslant i \leqslant k; 1 \leqslant j \leqslant m)$ nem mind $0$ skalárok, hogy $\sum_{i=1}^k \lambda_i \textbf{x}^{(i)}+\sum_{i=1}^m \mu_j \textbf{y}^{(j)}=\textbf{0}.$

    Az első szumma értéke legyen $\textbf{x}$, a másodiké $\textbf{y}$, ekkor $\textbf{x}\in S_1$ és $\textbf{y}\in S_2$.

    Ha $\textbf{x}=\textbf{0}$, akkor egyben $\textbf{y}=\textbf{0}$, és legalább az egyikük nemtriviális módon lett felírva a maga alterében, ami ellentmond annak, hogy az $\textbf{x}^{(i)}$ és az $\textbf{y}^{(j)}$ vektorok is lineárisan függetlenek.

    Ha $\textbf{x}\neq\textbf{0}$, akkor egyben $\textbf{y}\neq\textbf{0}$, és akkor e két vektor nem lesz lineárisan független egymástól, ellentmondva azon feltételnek, hogy egy $S_1$-beli és egy $S_2$-beli vektor mindig lineárisan független egymástól.

    Ez az ellentmondás bizonyítja az állítást.

  4. Adjuk meg az összes olyan $\textbf{B}$ mátrixot, amire az


    \begin{displaymath} \textbf{A}= \left( \begin{tabular}{rr} 1 & 0 \\ -1 & 0 \end{tabular} \right) \end{displaymath}

    mátrix esetén $\textbf{A}\textbf{B}=\textbf{B}\textbf{A}$ teljesül.

    Megoldás:

    A feltétel szerint a $\textbf{A}\textbf{B}=\textbf{B}\textbf{A}$ egyenlőség mindkét oldalán értelmes mátrixszorzás áll, így $\textbf{B}$ mérete feltétlenül 2x2.

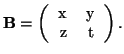    Legyen a keresett ${\bf B}$ mátrix $\textbf{B}= \left( \begin{tabular}{rr} x & y \\ z & t \end{tabular} \right).$ Az $\textbf{A}\textbf{B}$ és $\textbf{B}\textbf{A}$ szorzatok összevetéséből megállapítható, hogy a következő egyenlőségeknek kell teljesülniük:


    \begin{displaymath} x=x-y, \qquad y=0, \qquad -x=z-t,\qquad -y=0. \end{displaymath}

    Az első, a második és a negyedik egyenlet kielégítésének (szükséges és elégséges) feltétele egyaránt $y=0$.

    A harmadik egyenlet kielégítésének (szükséges és elégséges) feltétele $t=x+z$.

    A kért tulajdonsággal rendelkező mátrixok tehát pontosan azok, amelyek a következő alakban írhatók fel:


    \begin{displaymath} \textbf{B}= \left( \begin{tabular}{cc} x & 0 \\ z & x+z \end{tabular} \right). \end{displaymath}

  5. Adjuk meg $Im{\cal A}$ és $Ker{\cal A}$ egy-egy bázisát, ha az ${\cal A}$ lineáris leképezés $\textbf{A}$ mátrixa a következő:


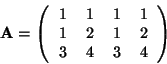
    \begin{displaymath} \textbf{A}= \left( \begin{tabular}{cccc} 1 & 1 & 1 & 1 \\ 1 & 2 & 1 & 2 \\ 3 & 4 & 3 & 4 \end{tabular} \right) \end{displaymath}

    Megoldás:

    Az $\textbf{A}$ mátrix első és harmadik, valamint második és negyedik oszlopa azonos, így $r(\textbf{A})\leqslant 2.$

    Az első és második oszlop nem többszörösei egymásnak, ezért a rang pontosan kettő.

    A képtér egy bázisát megadja a leképezés mátrixának oszlopaiból álló maximális lineárisan független rendszer.

    $Im{\cal A}$ bázisának jó lesz tehát az $(1,1,3)^T$ és $(1,2,4)^T$ oszlopvektorokból álló kételemű vektorrendszer.

    Mivel egy négydimenziós vektortérből képezünk egy kétdimenziós képtérbe, a Dimenziótétel alapján $dim(Ker{\cal A})=4-2=2$.

    Az $\textbf{A}$ mátrix alakjáról leolvasható, hogy a magtérnek eleme lesz minden $(a,b,-a,-b)^T$ alakú vektor. Mivel ezek egy kétdimenziós tér összes elemét adják, más vektor nem is tartozik a magtérbe.

    $Ker{\cal A}$ bázisának jó lesz tehát két lineárisan független, fenti alakú vektor, például $(1,1,-1,-1)^T$ és $(1,2,-1,-2)^T$.

  6. Hogyan változik meg egy $n$-szer $n$-es valós elemű mátrix determinánsa, ha minden elemét az ellentettjére cseréljük?

    Megoldás:

    A mátrix elemeit ellentettjükre cserélve a determinánst definiáló összegben szereplő minden szorzat minden tényezője az ellentettjére változik.

    Maguk a szorzatok tehát $(-1)^n$-szeresükre változnak.

    Mivel az összes szorzattal ez történik, ezek összege, tehát maga a determináns is $(-1)^n$-szeresére változik. (Vagyis páros $n$ esetén nem változik, páratlan $n$ esetén az ellentettjére vált.)

  7. Invertálhatók-e az alábbi mátrixok? Igen válasz esetén az inverzet is adjuk meg!


    1. \begin{displaymath} \textbf{A}= \left( \begin{tabular}{ccc} 2 & 4 & 2 \\ 3 & 7 & 2 \\ 5 & 5 & 10 \end{tabular} \right) \end{displaymath}


    2. \begin{displaymath} \textbf{B}= \left( \begin{tabular}{ccc} 1 & 0 & 0 \\ 0 & 2 & 6 \\ 0 & 4 & 1 \end{tabular} \right) \end{displaymath}

    Megoldás:

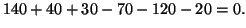
    1. A válasz: nem. Ez belátható például a determináns kiszámításával (a szorzások részletezése nélkül): $140+40+30-70-120-20=0.$
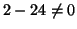    2. Igen. Ez is belátható a determináns kiszámításával (a szorzások részletezése nélkül): $2-24\neq 0$.

      Az inverz kereshető

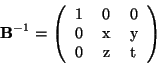
      \begin{displaymath} \textbf{B}^{-1}= \left( \begin{tabular}{ccc} 1 & 0 & 0 \\ 0 & x & y \\ 0 & z & t \end{tabular} \right) \end{displaymath}

      alakban. Látható ugyanis, hogy a B mátrix által megvalósított lineáris leképezés során a vektorok első koordinátája semmilyen kihatással nincs a másik két koordinátára és viszont, és ennek az inverzben is ugyanígy kell lennie.

      Az inverz keresett alakjában szereplő változókra a következő egyenlőségeknek kell teljesülni:


      \begin{displaymath} 2x+6z=1, \qquad 4x+z=0, \qquad 2y+6t=0, \qquad 4y+t=1. \end{displaymath}

      A másik irányból szorozva egy kicsit más, az előbbivel egyenértékű egyenletrendszer adódik:


      \begin{displaymath} 2x+4y=1, \qquad 6x+y=0, \qquad 2z+4t=0, \qquad 6z+t=1. \end{displaymath}

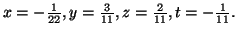
      A fenti egyenletrendszert (bármelyiket a kettő közül) megoldva a következő adódik: $x=-\frac{1}{22}, y=\frac{3}{11}, z=\frac{2}{11}, t=-\frac{1}{11}.$

  8. Bizonyítsuk be, hogy tetszőleges (de egymással összeszorozható) $\textbf{A}$ és $\textbf{B}$ mátrixokra


    \begin{displaymath} r(\textbf{A}\textbf{B}) \leqslant \min\{r(\textbf{A}), r(\textbf{B})\}. \end{displaymath}

    Megoldás:

    Az $\textbf{A}$ mátrixot tekinthetjük úgy, mint egy, a $\textbf{B}$ oszlopai által generált $V_B$ vektortérből való ${\cal A}$ leképezés mátrixát.

    Az $\textbf{A}\textbf{B}$ szorzatmátrix oszlopai által generált vektortér ekkor éppen $Im{\cal A}$, vagyis $r(\textbf{A}\textbf{B})=dim(Im{\cal A})$.

    A Dimenziótétel szerint $dim(Im{\cal A})=dim(V_B)-dim(Ker {\cal A})$, amiből következik, hogy $dim(Im{\cal A})\leqslant dim(V_B)$. Ugyanakkor $dim(V_B)$ definíció szerint egyenlő $r(\textbf{B})$-vel, vagyis az előbbi egyenlőtlenség úgy is írható, hogy $r(\textbf{A}\textbf{B})\leqslant r(\textbf{B})$.

    Ugyanezt az okfejtést megismételve úgy, hogy oszlopok helyett sorokat mondunk, és az $\textbf{A}$ és $\textbf{B}$ mátrix szerepét felcseréljük, kapható, hogy $r(\textbf{A}\textbf{B}) \leqslant r(\textbf{A})$. Ezzel tehát beláttuk, hogy $r(\textbf{A}\textbf{B})\leqslant \min\{r(\textbf{A}), r(\textbf{B})\}.$

Vissza