A logikai szita alkalmazása

Németh Zoltán




Feladat:

Adott egy szórakozott titkárnő, akinek az a feladata, hogy öt adott levelet tegyen bele a hozzájuk tartozó öt borítékba. Hányféleképpen tudja végrehajtani ezt a feladatot ,,teljesen rosszul'', azaz oly módon, hogy semelyik levél se a neki megfelelő borítékba kerüljön?

Megoldás:

Az összes lehetőség száma $ 5!=120$. Ebből kell levonnunk tehát a nekünk rossz esetek számát. Nekünk rossz elrendezés: amelyikben legalább egy levél a saját borítékjába kerül.

Számoljuk össze, hány ilyen elrendezés van. Az egy jó helyre kerülő levelet $ \binom{5}{1}$-féleképpen választhatjuk ki, ekkor a másik négy levél tetszőlegesen elrendezhető, erre $ 4!$ lehetőségünk van. A rossz esetek számára adódó eredmény tehát $ \binom{5}{1}4!$, ebben a pillanatban a feladatra adandó válasznak tehát $ 5! - \binom{5}{1}4!$ kínálkozik.

Ez a számítás azonban sánta. Jól számoltuk azon eseteket, amikor pontosan egy levél kerül jó helyre, de egynél többször vettünk számításba minden olyan elrendezést, amelyben egynél több levél kerül jó helyre. Így tehát a legalább két találatot tartalmazó elrendezéseket újra kell számolni.

Koncentráljunk most azon elrendezésekre, amelyekben pontosan kettő darab levél kerül jó helyre. Az összes esetek megszámolásakor ezeket egyszer számoltuk, az utána következő levonás során azonban kétszer. Azaz, mivel a végeredményben ezeket 0-szor számolva szeretnénk látni, az előbbi eredmény-jelölt kifejezéshez még egyszer hozzá kell adni ezeket az eseteket.

A pontosan két találatot tartalmazó esetek megszámolása helyett a legalább két találatot tartalmazó eseteket számoljuk meg. Az előbbihez hasonló gondolatmenetet követve válasszuk ki azt a két levelet, amelyek megfelelő borítékba kerülnek (erre $ \binom{5}{2}$ lehetőség van), a másik három levelet pedig rendezzük el tetszőlegesen (ez pedig nyilván $ 3!$-féleképp tehető meg). Vagyis azt kaptuk, hogy a legalább két találatot tartalmazó elrendezések száma $ \binom{5}{2}3!$.

A feladatra adandó válasz számításában ekkor a következő kifejezésnél tartunk: $ 5! - \binom{5}{1}4! + \binom{5}{2}3!$, de persze ezzel is baj van: a legalább három találatot tartalmazó elrendezéseket eddig minden csoportban többször számoltuk, tehát ezek biztosan nincsenek rendben.

A további gondolatmenet egyébként teljesen ugyanaz, mint az eddigiek, az egyértelműség kedvéért még egy iteráció kigondolását áttekintjük. Koncentráljunk most azokra az elrendezésekre, amelyekben pontosan három darab levél kerül jó helyre. Az összes esetek megszámolásakor ezeket egyszer vettük figyelembe. Utána minden ilyen esetet levontunk háromszor ( $ \binom{3}{1}$-szer), majd hozzáadtunk háromszor ( $ \binom{3}{2}$-ször). Vagyis most még 1-szer kell levonni.

Itt már érezhető az általánosítás: a pontosan $ k$ találatot tartalmazó eseteket az $ i$-edik lépésben pont $ \binom{k}{i}$-szer számolunk, a legutolsó alkalomra így $ \binom{k}{k}$, azaz 1 darab megszámolás marad. A darabszámokat - mint láttuk - váltakozó előjellel összegezzük, amely összeg: $ \sum_{i=1}^k(-1)^i\binom{k}{i}=0$ a binomiális tétel szerint. Persze épp a 0 összeg elérése a célunk, hisz ezeket az eseteket nem kívánjuk beleszámolni a végeredménybe, vagyis 0-szor akarjuk őket számolni.

Stb.

A végeredmény ezek alapján:

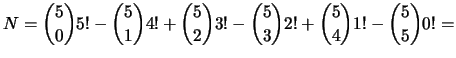
$\displaystyle N=\binom{5}{0}5! - \binom{5}{1}4! + \binom{5}{2}3! - \binom{5}{3}2! + \binom{5}{4}1! - \binom{5}{5}0! = $


$\displaystyle = 120-120+60-20+5-1 = 44.$

Mindez persze egyszerűbben is kijön, legalábbis n=5 esetén, lásd itt, ez a módszer azonban általánosítható n darab levél esetére is. A fentiekben vázolt gondolatmenet segítségével könnyű belátni, hogy a teljesen rossz elrendezések számának és az összes lehetséges elrendezés számának aránya 1/e-hez tart, ha n tart a végtelenhez.


[ BSz Fan Club ]