Komplex számok

1.
Bizonyítsuk be, hogy a következő dolgok felcserélhetők:
(a)
összeadás és konjugálás (azaz ${\overline{z_1}+\overline{z_2}=\overline{z_1+z_2}})$;
(b)
szorzás és konjugálás (azaz ${\overline{z_1}\cdot\overline{z_2}=\overline{z_1{\cdot}z_2}}$);
(c)
osztás és konjugálás.

2.
Határozzuk meg $\sqrt{5-12i}$ kanonikus alakját!

3.
Oldjuk meg az alábbi egyenleteket:
(a)
z2+3=0;
(b)
z2-5+12i=0;
(c)
z4-3z2-1=0;
(d)
$z+\overline{z}=2\vert z\vert$;
(e)
$\overline{z}=z^{1996}$.

4.
Mi a mértani helye a komplex számsíkon az $\frac{1+ti}{1-ti}$ alakú számoknak, ha tbefutja a valós számok halmazát? Ugyanez a kérdés, csak a vizsgálandó kifejezés legyen most $\frac{1+ti}{t+i}$.

5.
Mi |z|, |z1-z2|, iz geometriai jelentése? Milyen számokat kapunk, ha az a+bi komplex számnak megfelelő pontot tükrözzük
(a)
a valós tengelyre;
(b)
a képzetes tengelyre;
(c)
az y=x egyenletű egyenesre?

6.
Jellemezzük azon komplex számokat, melyeknek
(a)
összege valós;
(b)
szorzata valós;
(c)
négyzetösszege valós.

7.
Mi a szükséges és elégséges feltétele annak, hogy z1, z2, z3 egy egyenesbe essenek?

8.
Varázsoljuk trigonometrikus alakba az alábbi, kanonikus alakjaikkal megadott komplex számokat: 1+i, 5-12i, $\sqrt{3}-i$, $\sin\alpha-i\cos\alpha$.

9.
Mutassuk meg, hogy egységgyökök szorzata is egységgyök. Mi a feltétele annak, hogy egységgyökök összege is egységgyök legyen?

10.
Van-e a kilencedik egységgyökök között pontosan hat, melyek összege zérus? És pontosan hét?

11.
Bizonyítsuk be, hogy az 1995-ödik egységgyökök közül kiválasztható 876, melyek összege 0.

12.
Jelölje $e_0,e_1,\ldots, e_{n-1}$ az n-edik komplex egységgyököket. Kiszámítandó
(a)
$\sum_{i=0}^{n-1}e_i$;
(b)
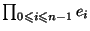
$\prod_{0\leqslant{i}\leqslant{n-1}}{e_i}$

13.
Legyen $z+z^{-1}=2\cos\alpha$. Mennyi z1997+z-1997 ?

14.
Legyen r pozitív egész. Bizonyítsuk be, hogy ha egy téglalap alakú sakktábla lefedhető $1\times{r}$-es dominókkal (egyrétűen és hézagmentesen), akkor a fedés egyállású dominókkal is elvégezhető.(${\star}$)

Vissza