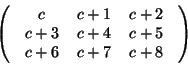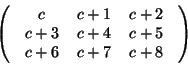Determinánsok, koordinátageometria II.

1.
Számítsuk ki az alábbi mátrixok determinánsát.

12 13
14 15
 
$\sin{x}$ $-\cos{x}$
$\cos{x}$ $\sin{x}$
 
1 2 3
2 3 1
3 1 2
 
1 7 -2
3 -4 1
11 2 -1

2.
Számítsuk ki az alábbi mátrixok determinánsát. A mátrix n*n-esek, a nem jelzett elemek értéke pedig 0.
(a)
a[i,i]=1
(b)
a[i,i]=A
(c)
$a[i,i]=a[i,i+1]=a[n,1]=1, \quad n=2k$
(d)
a[i,j]=i+j-1
(e)
a[i,j]=(i+j-1)2
(f)
$a[i,j]=\min (i,j)$
(g)
$a[i,j]={i+j-1 \choose i-1}$
(h)
$a[i,i]=2,\quad a[i,j]=1$
(i)
$a[i,i]=A,\quad a[i,j]=B$
(j)
a[i,j]=|i-j|
(k)
$a[i,j: i+j\leqslant n+1]=a[n,n]=1$
(l)
$a[i,i-1]=a[i,i+1]=1,\quad a[i,i]=2$
(m)
$a[i,i-1]=a[i,i+1]=-1,\quad a[i,i]=1$

3.
Egy n*n-es mátrix 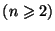$(n\geqslant 2)$ minden eleme 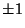$\pm{1}$. Igazoljuk, hogy determinánsa osztható 2n-1-nel.

4.
Megválasztható-e c értéke úgy, hogy az alábbi mátrix determinánsa ne nulla legyen?

\begin{displaymath}\left( \begin{array}{ccccccc} ~ & c & ~ & c+1 & ~ & c+2 & ~ ... ...c+5 & ~ \\ ~ & c+6 & ~ & c+7 & ~ & c+8 & ~ \end{array} \right)\end{displaymath}

5.
Van egy nxn-es mátrixunk, melynek az elemei egy kivételével rögzítettek. Igaz-e, hogy az utolsó elem mindig megválasztható úgy, hogy az így kitöltött mátrix determinánsa 0 legyen?

6.
A pontos érték meghatározása nélkül mutassuk meg, hogy az alábbi determináns értéke nem zérus.
1222 1492 1956 1789
1456 1000 1867 1686
1848 1945 1552 1640
1769 1514 1918 1812

7.
Egy n*n-es mátrix minden eleme egyjegyű, így sorai n jegyű pozitív egész számokként is olvashatók. Mi több, az így kapott számok mindegyike osztható 1999-cel. Igaz-e, hogy a determinánsa is osztható 1999-cel?($\star$)

8.
Egy n*n-es mátrix minden eleme véletlenszerűen 0 vagy 1. Mennyi annak a valószínűsége, hogy a mátrix determinánsa 0?($\star$$\star$)
9.
Határozzuk meg a P1(-1,-2,-3) és a P2(1,4,7) pontokon átmenő egyenes egyenletrendszerét.

10.
Határozzuk meg a p paraméter értékét úgy, hogy az alábbi két (egyenletrendszereikkel megadott) egyenesnek legyen közös pontja!


\begin{displaymath}\frac{x-1}{7}=\frac{y-6}{2}=\frac{z+3}{4}\end{displaymath}

és

\begin{displaymath}\frac{x+2}{2}=\frac{y}{3};z=p.\end{displaymath}

Vissza