


Next: About this document ...
Számítástudomány elemei gyakorlat
8. feladatsor (2002. okt. 31.)
- Legyenek egy
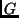 gráf pontjai az
gráf pontjai az 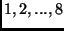 számok, és az
számok, és az
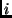 és a
és a 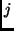 csúcs pontosan akkor legyen összekötve, ha
csúcs pontosan akkor legyen összekötve, ha
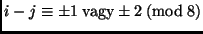 . Határozzuk
meg
. Határozzuk
meg 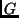 kromatikus számát,
kromatikus számát, 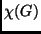 -t! (ZH, 2002. máj.)
-t! (ZH, 2002. máj.)
- Igaz-e, hogy ha egy
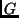 gráf
gráf 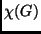 kromatikus számára és
kromatikus számára és
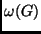 klikkszámára teljesül, hogy
klikkszámára teljesül, hogy
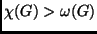 , akkor
behúzhatók
, akkor
behúzhatók 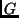 -be új élek úgy, hogy a keletkező
-be új élek úgy, hogy a keletkező 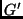 gráfra
gráfra
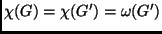 teljesüljön?
teljesüljön?
- Egy négyzetrácsban legyen egy lépés, hogy egy négyzetből
átmehetünk egy vele közös éllel rendelkező négyzetbe. A
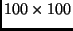 -as rácsban mi az a legkevesebb szín, amivel a négyzetek
kiszínezhetők úgy, hogy az egymásból pontosan két lépéssel
elérhető négyzetek színe különböző? (ZH, 1999. máj.)
-as rácsban mi az a legkevesebb szín, amivel a négyzetek
kiszínezhetők úgy, hogy az egymásból pontosan két lépéssel
elérhető négyzetek színe különböző? (ZH, 1999. máj.)
- Legyen
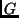 véges egyszerű gráf, kromatikus száma
véges egyszerű gráf, kromatikus száma 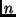 .
Tekintsük
.
Tekintsük 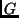 -nek egy
-nek egy 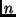 színnel való jó színezését, melyben a
használt színek egyike piros. Bizonyítsuk be, hogy a megadott
színezésben van olyan piros színű pont, amelynek a szomszédai
között az összes felhasznált pirostól különböző szín előfordul!
(Vizsga, 2000. aug.)
színnel való jó színezését, melyben a
használt színek egyike piros. Bizonyítsuk be, hogy a megadott
színezésben van olyan piros színű pont, amelynek a szomszédai
között az összes felhasznált pirostól különböző szín előfordul!
(Vizsga, 2000. aug.)
- Legyen a
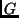 gráf ponthalmaza
gráf ponthalmaza
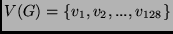 . A
. A 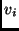 és a
és a 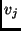 pontok között
akkor és csak akkor van él, ha
pontok között
akkor és csak akkor van él, ha
- az indexek közül a nagyobbikat a kisebbikkel elosztva
kettőhatványt kapunk;
- a kisebb index osztója a nagyobb
indexnek.
Határozzuk meg 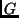 kromatikus számát!
kromatikus számát!
- A
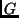 egyszerű
egyszerű 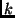 -reguláris gráf élkromatikus száma
-reguláris gráf élkromatikus száma
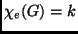 . Bizonyítsuk be, hogy ekkor
. Bizonyítsuk be, hogy ekkor 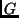 -ben létezik teljes
párosítás! (ZH, 2001. okt.)
-ben létezik teljes
párosítás! (ZH, 2001. okt.)
- Bergengóciában 1, 2, 3 és 5 petákos érméket használnak.
Mindegyik annyi gramm tömegű, ahány petákot ér. Van
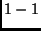 érménk
mindegyikből, de az egyik hamis: tömege eltér a valódiétól.
Kétkarú mérleggel hány méréssel állapíthatjuk meg, hogy
érménk
mindegyikből, de az egyik hamis: tömege eltér a valódiétól.
Kétkarú mérleggel hány méréssel állapíthatjuk meg, hogy
- melyik a hamis?
- melyik a hamis, és könnyebb vagy
nehezebb, mint a valódi?
- Legyen
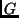 egy
egy 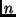 pontú irányítatlan egyszerű összefüggő
gráf, és jelölje
pontú irányítatlan egyszerű összefüggő
gráf, és jelölje 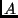 a
a 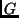 szomszédsági mátrixát. Bizonyítsuk be,
hogy minden
szomszédsági mátrixát. Bizonyítsuk be,
hogy minden
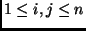 számpárhoz létezik olyan
számpárhoz létezik olyan 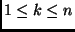 , hogy az
, hogy az 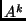 mátrix
mátrix 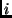 -edik sorának
-edik sorának 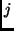 -edik eleme nem
nulla. (Pótzh, 2001. máj.)
-edik eleme nem
nulla. (Pótzh, 2001. máj.)
- Az alábbi mátrixok közül melyek állnak elő gráfok
körmátrixaként?
- Egy labdarúgó bajnokságban 10 csapat játszik körmérkőzést.
Minden fordulóban minden csapat pályára lép. Igazoljuk, hogy a
4. forduló után van három olyan csapat, amelyik egyike sem
játszott még a másikkal! (A feladatra nov. 14-ig beadott helyes
megoldás csokit ér!)



Next: About this document ...
Veto Balint
2002-10-31

