Next: About this document ...
Számítástudomány elemei gyakorlat
3. feladatsor (2002. szept. 26.)
Az előző óráról maradt:
- Egy teljes gráf ponthalmaza
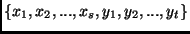 . Az
. Az
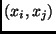 élek költsége (súlya) 1 Ft, az
élek költsége (súlya) 1 Ft, az
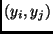 éleké 2 Ft,
az
éleké 2 Ft,
az
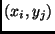 éleké pedig 3 Ft. Mennyibe kerül a
legolcsóbb feszítőfa? (ZH, 2000. márc.)
éleké pedig 3 Ft. Mennyibe kerül a
legolcsóbb feszítőfa? (ZH, 2000. márc.)
- Hány olyan fa adható meg az
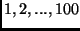 csúcsokon, melynek
van olyan éle, amit elhagya a maradék gráf két komponensének
pontjai rendre az
csúcsokon, melynek
van olyan éle, amit elhagya a maradék gráf két komponensének
pontjai rendre az 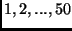 ill. az
ill. az 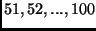 csúcsok?
csúcsok?
Új feladatok:
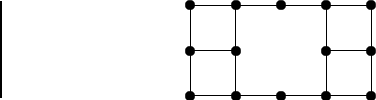
- Van-e az alábbi gráfnak Hamilton-köre ill. -útja? (Vizsga,
2001. jún.)
- Hány Hamilton-köre ill. -útja van a
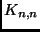 teljes páros
gráfnak? (Vizsga, 1999. máj.)
teljes páros
gráfnak? (Vizsga, 1999. máj.)
- A
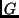 3-reguláris egyszerű gráfra teljesül, hogy
3-reguláris egyszerű gráfra teljesül, hogy
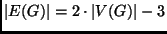 . Bizonyítsuk be, hogy
. Bizonyítsuk be, hogy 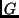 -ben van
Hamilton-kör! (ZH, 1999. márc.)
-ben van
Hamilton-kör! (ZH, 1999. márc.)
- A
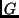 egyszerű gráf pontjai az
egyszerű gráf pontjai az 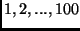 számok. Az
számok. Az 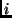 és
és 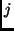 pontok pontosan akkor vannak éllel összekötve, ha
pontok pontosan akkor vannak éllel összekötve, ha
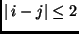 . Van-e
. Van-e 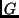 -ben Euler-kör ill. Euler-út? (ZH, 2000.
márc.)
-ben Euler-kör ill. Euler-út? (ZH, 2000.
márc.)
- A
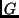 gráf pontjai egy 10 elemű halmaz 2 elemű
részhalmazainak felelnek meg. Két pont akkor van összekötve éllel,
ha a pontoknak megfelelő két részhalmaz diszjunkt. Van-e a
gráf pontjai egy 10 elemű halmaz 2 elemű
részhalmazainak felelnek meg. Két pont akkor van összekötve éllel,
ha a pontoknak megfelelő két részhalmaz diszjunkt. Van-e a
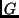 gráfban Euler- ill. Hamilton-kör? (Pótzh, 1999. máj.)
gráfban Euler- ill. Hamilton-kör? (Pótzh, 1999. máj.)
- Egy 12 fős társaságban mindenki legalább 6 embert ismer (az
ismeretség kölcsönös). Bizonyítsuk be, hogy a társaság leültethető
egy kerek asztal köré úgy, hogy mindenki ismerje a szomszédait!
(Pótzh, 2001. dec.)
- A
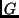 összefüggő gráfban minden pont foka páros. Bizonyítsa
be, hogy ha
összefüggő gráfban minden pont foka páros. Bizonyítsa
be, hogy ha 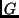 -nek páros sok éle van, akkor létezik
-nek páros sok éle van, akkor létezik 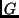 -nek olyan
-nek olyan
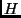 részgráfja, hogy
részgráfja, hogy 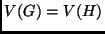 , és minden pont
, és minden pont 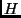 -beli foka
éppen fele a
-beli foka
éppen fele a 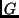 -beli fokának. (ZH, 2000. máj.)
-beli fokának. (ZH, 2000. máj.)
- Legyen
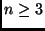 és legyen a
és legyen a 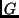 gráf pontjainak halmaza az
gráf pontjainak halmaza az
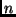 hosszúságú
hosszúságú 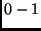 sorozatok halmaza. A gráf két pontja között
akkor és csak akkor van él, ha a nekik megfelelő két sorozat
legalább 2 helyen eltér. Milyen
sorozatok halmaza. A gráf két pontja között
akkor és csak akkor van él, ha a nekik megfelelő két sorozat
legalább 2 helyen eltér. Milyen 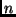 esetén van
esetén van 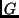 -ben
Euler-körséta? (Vizsga, 2000. jún.)
-ben
Euler-körséta? (Vizsga, 2000. jún.)



Next: About this document ...
Veto Balint
2002-10-10