


Next: About this document ...
Számítástudomány elemei gyakorlat
12. feladatsor (2002. nov. 28.)
- (ism.) Bizonyítsuk be, hogy tetszőleges
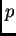 prímre
prímre
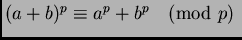 !
!
- (ism.) Bizonyítsuk az ismert 9-cel való oszthatósági
szabályt! (Útmutatás: legyen
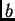 10-es számrendszerbeli felírása
10-es számrendszerbeli felírása
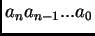 , ekkor igazoljuk, hogy
, ekkor igazoljuk, hogy
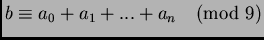 teljesül.)
teljesül.)
- Bizonyítsuk be, hogy a
halmaz (vagyis az összes komplex egységgyök) a komplex számok
szorzására nézve Abel-csoportot alkot! (Vizsga, 2000. máj.)
- Bizonyítsuk be, hogy az
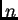 elem összes permutációi által
alkotott csoportban (az
elem összes permutációi által
alkotott csoportban (az 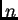 -edfokú szimmetrikus csoportban, azaz
-edfokú szimmetrikus csoportban, azaz
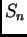 -ben) az 1-es elemet helyben hagyó permutációk részcsoportot
alkotnak! (Vizsga, 2001. jún.)
-ben) az 1-es elemet helyben hagyó permutációk részcsoportot
alkotnak! (Vizsga, 2001. jún.)
- Álljon
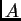 azokból a
azokból a 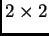 -es mátrixokból, melyeknek
mind a négy eleme ugyanaz a pozitív valós szám. Csoportot alkot-e
ez a halmaz a szokásos mátrixszorzással?
-es mátrixokból, melyeknek
mind a négy eleme ugyanaz a pozitív valós szám. Csoportot alkot-e
ez a halmaz a szokásos mátrixszorzással?
(Pótzh, 2001. máj.)
- Hány hatodrendű elem van
- a 24 rendű ciklikus csoportban,
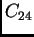 -ben?
-ben?
- a szabályos tízszög szimmetriacsoportjában,
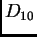 -ben?
(Vizsga, 2001. jún.)
-ben?
(Vizsga, 2001. jún.)
- Mutassuk meg, hogy végtelen sok
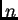 pozitív egész számra
teljesül, hogy az
pozitív egész számra
teljesül, hogy az 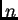 elemű csoportok izomorfak!
elemű csoportok izomorfak!
- Bizonyítsuk be, hogy egy
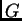 csoport tetszőleges
csoport tetszőleges 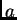 elemének rendje megegyezik
elemének rendje megegyezik 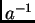 , vagyis
, vagyis 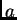 inverzének
rendjével!
inverzének
rendjével!
- Csoportot alkotnak-e a valós számok az
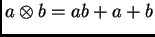 -vel definiált műveletre? (Vizsga, 2002. jan.)
-vel definiált műveletre? (Vizsga, 2002. jan.)



Next: About this document ...
Veto Balint
2002-11-28
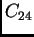 -ben?
-ben?
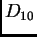 -ben?
(Vizsga, 2001. jún.)
-ben?
(Vizsga, 2001. jún.)