


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
8. feladatsor (2002. ápr. 12.)
- Keresd meg az alábbi mátrixok sajátértékeit és a hozzájuk tartozó
sajátvektorokat (vagyis határozd meg a sajátaltereket)!
- Legyen
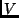 a síkvektorok szokásos vektortere. Határozd meg
a síkvektorok szokásos vektortere. Határozd meg 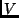 következő
lineáris transzformációinak sajátértékeit, sajátvektorait és a karakterisztikus
polinomot!
következő
lineáris transzformációinak sajátértékeit, sajátvektorait és a karakterisztikus
polinomot!
- origó körüli
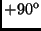 -os forgatás;
-os forgatás;
-
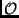 leképezés (minden vektorhoz a
leképezés (minden vektorhoz a
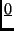 -t rendeli);
-t rendeli);
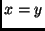 egyenesre való vetítés.
egyenesre való vetítés.
- Melyek igazak az alábbi állítások közül (tetszőleges vektortérben)? (
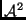 az
az
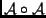 leképezést jelöli,
leképezést jelöli,
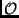 pedig a null-leképezést, mely minden vektorhoz
a
pedig a null-leképezést, mely minden vektorhoz
a
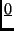 -t rendeli)
-t rendeli)
- Ha
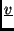 sajátvektora
sajátvektora
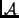 -nak, akkor
-nak, akkor
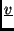 sajátvektora
sajátvektora
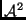 -nek;
-nek;
- Ha
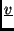 sajátvektora
sajátvektora
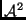 -nek, akkor
-nek, akkor
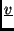 sajátvektora
sajátvektora
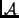 -nak;
-nak;
- Ha 0 sajátértéke
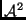 -nek, akkor 0 sajátértéke
-nek, akkor 0 sajátértéke
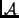 -nak;
-nak;
- Ha
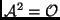 , akkor
, akkor
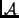 -nak a 0 az egyetlen sajátértéke.
-nak a 0 az egyetlen sajátértéke.
- Végezd el az alábbi műveleteket!
- Oldd meg a komplex számok halmazán a következő egyenleteket:
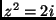
-
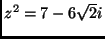
-
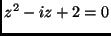 (ZH. 2000. nov.)
(ZH. 2000. nov.)
- Ábrázold a komplex számsík azon
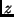 pontjainak halmazát, melyre teljesül:
pontjainak halmazát, melyre teljesül:
-
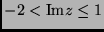
-
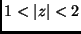
-
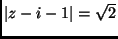
- Van-e a közönséges síkban ill. térben olyan lineáris transzformáció, melynek
nincs valós sajátvektora?
- ** Berci vett egy doboz Mackósajtot, melyben 6 db
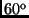 -os körcikk
alakú sajt található. Este megevett belőlük hármat, és betette a hűtőbe. Reggel, mikor
felnyitotta a dobozt, azt vette észre, hogy ha az egyes sajtcikkek körívre eső csúcsait a körön
végighaladva
-os körcikk
alakú sajt található. Este megevett belőlük hármat, és betette a hűtőbe. Reggel, mikor
felnyitotta a dobozt, azt vette észre, hogy ha az egyes sajtcikkek körívre eső csúcsait a körön
végighaladva 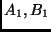 -gyel,
-gyel, 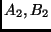 -vel, ill.
-vel, ill. 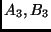 -mal jelöljük, akkor a
-mal jelöljük, akkor a
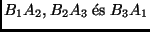 szakaszok felezőpontjai szabályos háromszöget
alkotnak. (A körcikkek csúcsai továbbra is a kör középpontjában helyezkednek
el.) Bizonyítsd be, hogy Berci megfigyelése helyes, függetlenül attól, hogy a
sajtok egymással milyen szöget zárnak be! (Ápr. 26-áig beadott helyes
megoldások csokit érnek!)
szakaszok felezőpontjai szabályos háromszöget
alkotnak. (A körcikkek csúcsai továbbra is a kör középpontjában helyezkednek
el.) Bizonyítsd be, hogy Berci megfigyelése helyes, függetlenül attól, hogy a
sajtok egymással milyen szöget zárnak be! (Ápr. 26-áig beadott helyes
megoldások csokit érnek!)



Next: About this document ...
Veto Balint
2002-04-10

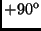 -os forgatás;
-os forgatás;
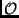 leképezés (minden vektorhoz a
leképezés (minden vektorhoz a
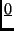 -t rendeli);
-t rendeli);
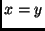 egyenesre való vetítés.
egyenesre való vetítés.
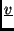 sajátvektora
sajátvektora
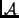 -nak, akkor
-nak, akkor
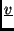 sajátvektora
sajátvektora
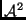 -nek;
-nek;
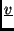 sajátvektora
sajátvektora
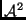 -nek, akkor
-nek, akkor
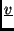 sajátvektora
sajátvektora
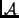 -nak;
-nak;
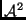 -nek, akkor 0 sajátértéke
-nek, akkor 0 sajátértéke
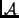 -nak;
-nak;
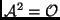 , akkor
, akkor
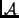 -nak a 0 az egyetlen sajátértéke.
-nak a 0 az egyetlen sajátértéke.
![$\displaystyle \left.a\right)\sqrt{-5}\hspace{4cm} \left.b\right)\sqrt{2+\sqrt{12}i} \hspace{4cm}
\left.c\right)\sqrt[4]{3+3i}\hspace{4cm}
$](img12.png)
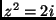
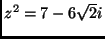
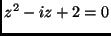 (ZH. 2000. nov.)
(ZH. 2000. nov.)