


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
6. feladatsor (2002. márc. 29.)
- Számítsuk ki az alábbi mátrixok rangját (a paraméter függvényében):
- Legyen
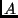 egy
egy 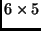 -ös valós mátrix. Melyek igazak a következő
állítások közül?
-ös valós mátrix. Melyek igazak a következő
állítások közül?
- Ha az első három sor lineárisan összefüggő, akkor a bal felső
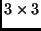 -as aldetermináns 0.
-as aldetermináns 0.
- Ha a bal felső
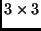 -as aldetermináns 0, akkor az első három sor
lineárisan összefüggő.
-as aldetermináns 0, akkor az első három sor
lineárisan összefüggő.
- Ha az első három oszlop lineárisan összefüggő, és az utolsó három oszlop
is lineárisan összefüggő, akkor
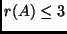 .
.
- Ha az első két oszlop lineárisan összefüggő, és az utolsó két oszlop
is lineárisan összefüggő, akkor
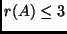 .
.
- Legyen
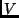 a síkvektorok szokásos vektortere. Döntsük el az alábbi
hozzárendelésekről, hogy lineáris leképezések-e! Ha igen, írjuk fel
a mátrixukat az
a síkvektorok szokásos vektortere. Döntsük el az alábbi
hozzárendelésekről, hogy lineáris leképezések-e! Ha igen, írjuk fel
a mátrixukat az
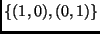 bázisban! Minden
bázisban! Minden
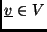 vektornak
feleltessük meg
vektornak
feleltessük meg
- az
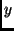 tengelyre való tükörképét.
tengelyre való tükörképét.
- origó körüli
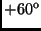 -os elforgatottját.
-os elforgatottját.
- az
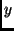 tengelyre való tükörképének origó körüli
tengelyre való tükörképének origó körüli
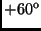 -os
elforgatottját.
-os
elforgatottját.
- azt az
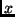 tengelyre eső vektort, amelynek első koordinátája a
tengelyre eső vektort, amelynek első koordinátája a
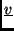 koordinátái közül a nagyobb.
koordinátái közül a nagyobb.
- azt az
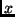 tengelyre eső vektort, amelynek első koordinátája a
tengelyre eső vektort, amelynek első koordinátája a
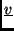 koordinátáinak összege.
koordinátáinak összege.
- Legyen
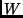 a
a 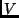 vektortér egy nemtriviális altere. Lineáris transzformációt
definiálnak-e az alábbi megfeleltetések?
vektortér egy nemtriviális altere. Lineáris transzformációt
definiálnak-e az alábbi megfeleltetések?
- Tekintsük a legfeljebb harmadfokú, valós együtthatós polinomokat
(azaz az
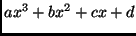 alakú kifejezéseket, ahol
alakú kifejezéseket, ahol
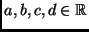 ).
Ezeket értelemszerűen össze tudjuk adni, vagy meg tudjuk szorozni egy
valós számmal. így egy
).
Ezeket értelemszerűen össze tudjuk adni, vagy meg tudjuk szorozni egy
valós számmal. így egy 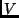 vektorteret kapunk. (A műveletek tehát ugyanúgy
működnek, mint a valós számnégyesekből álló vektortérben.)
vektorteret kapunk. (A műveletek tehát ugyanúgy
működnek, mint a valós számnégyesekből álló vektortérben.) 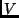 -ben egy
bázis a
-ben egy
bázis a
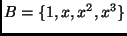 halmaz. Döntsd el, hogy az alábbi
halmaz. Döntsd el, hogy az alábbi
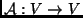 függvények lineáris leképezések-e? Ha igen, add meg a kép-
és magterüket, illetve a mátrixukat a
függvények lineáris leképezések-e? Ha igen, add meg a kép-
és magterüket, illetve a mátrixukat a 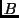 bázisban felírva!
Minden polinomnak feletessük meg
bázisban felírva!
Minden polinomnak feletessük meg
- a konstans tagját;
- a deriváltját.
- Hány olyan
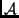 lineáris transzformáció van az
lineáris transzformáció van az
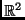 vektortéren, amelyre
vektortéren, amelyre
-
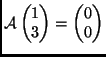 és
és
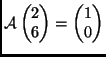 ;
;
-
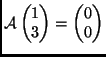 és
és
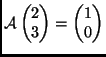 ;
;
-
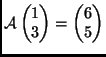 és
és
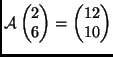 ;
;
- Legyen
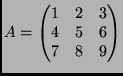 .
A tér minden
.
A tér minden
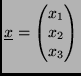 vektorához rendeljük hozzá a tér
vektorához rendeljük hozzá a tér
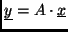 vektorát! (A tér vektorai tehát
vektorát! (A tér vektorai tehát 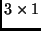 -es
mátrixok.)
-es
mátrixok.)
- Bizonyítsd be, hogy így egy
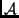 lineáris transzformációt kaptunk.
lineáris transzformációt kaptunk.
- Írd fel
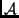 mátrixát az
mátrixát az
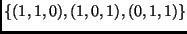 bázisban.
bázisban.
- Határozd meg Ker
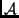 -t és Im
-t és Im
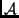 -t.
-t.



Next: About this document ...
Veto Balint
2002-03-25

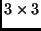 -as aldetermináns 0.
-as aldetermináns 0.
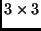 -as aldetermináns 0, akkor az első három sor
lineárisan összefüggő.
-as aldetermináns 0, akkor az első három sor
lineárisan összefüggő.
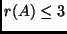 .
.
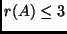 .
.
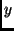 tengelyre való tükörképét.
tengelyre való tükörképét.
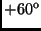 -os elforgatottját.
-os elforgatottját.
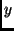 tengelyre való tükörképének origó körüli
tengelyre való tükörképének origó körüli
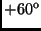 -os
elforgatottját.
-os
elforgatottját.
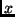 tengelyre eső vektort, amelynek első koordinátája a
tengelyre eső vektort, amelynek első koordinátája a
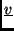 koordinátái közül a nagyobb.
koordinátái közül a nagyobb.
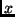 tengelyre eső vektort, amelynek első koordinátája a
tengelyre eső vektort, amelynek első koordinátája a
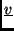 koordinátáinak összege.
koordinátáinak összege.

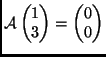 és
és
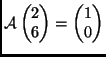 ;
;
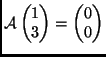 és
és
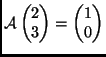 ;
;
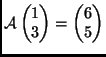 és
és
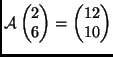 ;
;
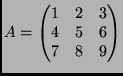 .
A tér minden
.
A tér minden
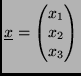 vektorához rendeljük hozzá a tér
vektorához rendeljük hozzá a tér
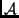 lineáris transzformációt kaptunk.
lineáris transzformációt kaptunk.
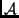 mátrixát az
mátrixát az
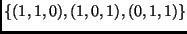 bázisban.
bázisban.
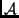 -t és Im
-t és Im
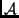 -t.
-t.