


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
4. feladatsor (2002. márc. 8.)
- Mennyi az 1, 2, ...,
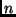 elemek inverziószáma az alábbi permutációkban?
elemek inverziószáma az alábbi permutációkban?
- 1, 3, 5, 7, 9, 8, 6, 4, 2 (n=9)
- 100, 101, 98, 99, 96, 97, ..., 2, 3, 1 (n=101)
- Tekintsük az alábbi determinánst!
Mi lesz ebben a definíció szerinti kiszámoláskor az alábbi szorzatok
előjele?
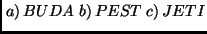
- Számold ki az alábbi determinánsokat!
- Legyen
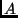 egy
egy 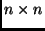 -es mátrix. Bizonyítsd be, hogy az oszlopai
(mint függőlegesen írt oszlopvektorok) akkor és csak akkor lineárisan
függetlenek, ha det
-es mátrix. Bizonyítsd be, hogy az oszlopai
(mint függőlegesen írt oszlopvektorok) akkor és csak akkor lineárisan
függetlenek, ha det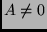 .
.
- Az
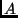 és a
és a 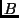
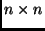 -es mátrixról tudjuk, hogy det
-es mátrixról tudjuk, hogy det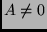 ,
valamint azt, hogy
,
valamint azt, hogy
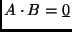 . Határozd meg a
. Határozd meg a 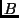 mátrixot!
(Itt a
mátrixot!
(Itt a
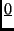 a csupa nulla mátrixot jelöli.)
a csupa nulla mátrixot jelöli.)
- Határozd meg az összes olyan
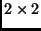 -es
-es 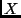 mátrixot, melynek minden
eleme racionális szám és amelyre
mátrixot, melynek minden
eleme racionális szám és amelyre
![$ X^{2001}=\left[\begin{matrix}1&3\ 2&8
\end{matrix}\right]$](img14.png) teljesül.
teljesül.
- Legyen
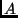 egy
egy 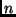 sorból és
sorból és 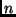 oszlopból álló valós mátrix, a
oszlopból álló valós mátrix, a 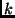 -adik
sorának
-adik
sorának 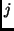 -edik elemét jelölje
-edik elemét jelölje 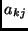 . Legyen
. Legyen 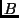 az az
az az 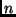 -szer
-szer 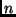 -es
mátrix, amelyben a
-es
mátrix, amelyben a 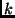 -adik sor
-adik sor 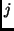 -edik elemére
-edik elemére
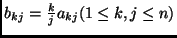 . Mennyi
. Mennyi 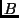 determinánsa, ha tudjuk, hogy det
determinánsa, ha tudjuk, hogy det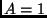 ?
(ZH. 2000. nov.)
?
(ZH. 2000. nov.)
- Bizonyítsd be, hogy
- Egy
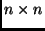 -es mátrix minden eleme 1 vagy -1. Igazoljuk,
hogy a mátrix determinánsa osztható
-es mátrix minden eleme 1 vagy -1. Igazoljuk,
hogy a mátrix determinánsa osztható 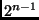 -nel. (Vizsga, 2001. dec.)
-nel. (Vizsga, 2001. dec.)



Next: About this document ...
Veto Balint
2002-03-05



![$ X^{2001}=\left[\begin{matrix}1&3\ 2&8
\end{matrix}\right]$](img14.png) teljesül.
teljesül.




![$ X^{2001}=\left[\begin{matrix}1&3\ 2&8
\end{matrix}\right]$](img14.png) teljesül.
teljesül.
