


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
2. feladatsor (2002. febr. 22.)
- Számítsuk ki az
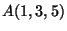 , a
, a 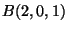 és a
és a 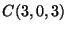 pontok által
meghatározott háromszög
pontok által
meghatározott háromszög 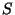 súlypontját! Határozzuk meg a térnek azon
pontjait, melyek rajta vannak az
súlypontját! Határozzuk meg a térnek azon
pontjait, melyek rajta vannak az 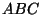 síkra az
síkra az 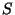 pontban állított
megőleges egyenesen! (Vizsga, 2001. jan.)
pontban állított
megőleges egyenesen! (Vizsga, 2001. jan.)
- A valós együtthatós polinomok vektorterében alteret alkotnak-e az alábbi
tulajdonságokkal rendelkező
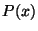 polinomokból álló halmazok:
polinomokból álló halmazok:
- deg
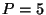
- deg
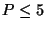
- deg
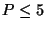 és
és 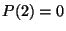
- deg
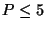 és
és 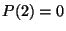 vagy
vagy 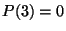
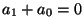 , ahol
, ahol 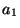 az elsőfokú tag együtthatója,
az elsőfokú tag együtthatója, 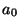 pedig a konstans
tag
pedig a konstans
tag
-
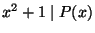
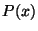 -nek van valós gyöke
-nek van valós gyöke
- Legyen
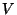 vektortér, és
vektortér, és 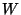 a
a 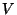 egy nemtriviális altere. Melyek igazak
az alábbi állítások közül (
egy nemtriviális altere. Melyek igazak
az alábbi állítások közül (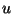 ,
, 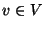 ,
, 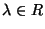 )?
)?
-
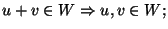
-

-
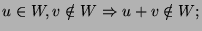
-
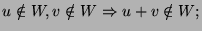
-
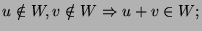
- A valós számhármasok vektorterében alteret alkotnak-e azok az
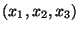 vektorok, melyekre
vektorok, melyekre 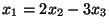 ? (ZH, 2000. nov.)
? (ZH, 2000. nov.)
- Döntsük el az alábbi állításokról, hogy igazak-e (a 3 dimenziós térben)?
-
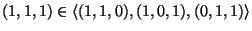
- Az
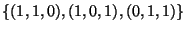 vektorok generátorrendszert alkotnak.
vektorok generátorrendszert alkotnak.
- Az
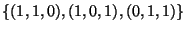 vektorok lineárisan függetlenek.
vektorok lineárisan függetlenek.
- Az
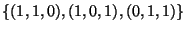 vektorok bázist (lineárisan független
generátorrendszert) alkotnak.
vektorok bázist (lineárisan független
generátorrendszert) alkotnak.
- A
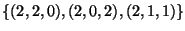 vektorok generátorrendszert alkotnak.
vektorok generátorrendszert alkotnak.
- A
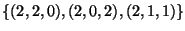 vektorok lineárisan függetlenek.
vektorok lineárisan függetlenek.
- Melyek igazak az alábbi állítások közül? (A vektorok egy tetszőleges
vektortérből valók.)
- Ha
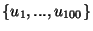 lineárisan független és
lineárisan független és
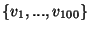 is
lineárisan független, akkor
is
lineárisan független, akkor
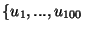 ,
,
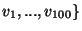 is
lineárisan független.
is
lineárisan független.
- Ha
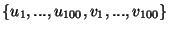 lineárisan független, akkor
lineárisan független, akkor
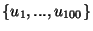 és
és
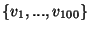 is lineárisan független.
is lineárisan független.
- Ha
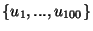 lineárisan független és
lineárisan független és
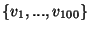 is
lineárisan független, akkor
is
lineárisan független, akkor 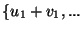 ,
,
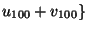 is lineárisan
független.
is lineárisan
független.
- Ha
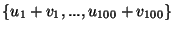 lineárisan független, akkor
lineárisan független, akkor
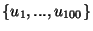 és
és
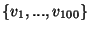 is lineárisan független.
is lineárisan független.
- Ha
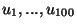 közül bármely 99 vektor lineárisan független,
akkor
közül bármely 99 vektor lineárisan független,
akkor
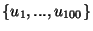 is lineárisan független.
is lineárisan független.
- Ha
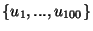 lineárisan független, akkor
lineárisan független, akkor
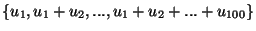 is lineárisan független.
is lineárisan független.
- Tegyük fel, hogy egy
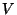 vektortér
vektortér 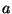 ,
, 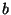 ,
, 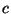 és
és 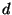 elemeire
elemeire
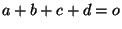 teljesül. (
teljesül. (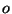 a vektortér nulleleme.) Melyek igazak az alábbiak
közül?
a vektortér nulleleme.) Melyek igazak az alábbiak
közül?
-
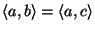
-
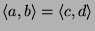
-
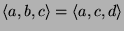
-
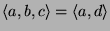
-
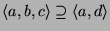
- Tegyük fel, hogy egy
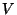 vektortér
vektortér 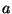 ,
, 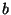 és
és 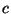 elemeire
elemeire
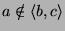 ,
,
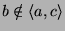 és
és
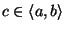 . Határozzuk meg a
. Határozzuk meg a 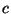 vektort!
vektort!
- Legyenek
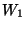 ,
, 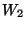 és
és 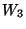 alterek
alterek 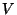 -ben. Milyen kapcsolatban áll
egymással
-ben. Milyen kapcsolatban áll
egymással
-
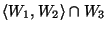 és
és
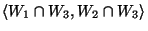 ;
;
-
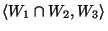 és
és
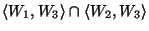 ;
;
-
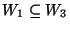 esetén
esetén
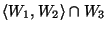 és
és
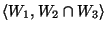 ?
?
- Legyenek
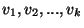 lineárisan független vektorok. Adjuk meg a
lineárisan független vektorok. Adjuk meg a 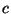 paraméter összes olyan valós értékét, melyre a
paraméter összes olyan valós értékét, melyre a
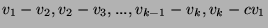 vektorok lineárisan függetlenek!
(ZH. 1998. nov.)
vektorok lineárisan függetlenek!
(ZH. 1998. nov.)
- Egy tetszőleges
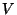 vektortérben adott 2001 darab vektor, amelyekről tudjuk,
hogy generátorrendszert alkotnak. Bizonyítsd be, hogy kiválsztható közülük
néhány (esetleg mind, esetleg csak egy) úgy, hogy a kiválasztott vektorok
bázist alkotnak!
vektortérben adott 2001 darab vektor, amelyekről tudjuk,
hogy generátorrendszert alkotnak. Bizonyítsd be, hogy kiválsztható közülük
néhány (esetleg mind, esetleg csak egy) úgy, hogy a kiválasztott vektorok
bázist alkotnak!
- Bizonyítsuk be, hogy ha egy vektortérnek van nemtriviális altere, akkor
végtelen sok altere van!



Next: About this document ...
Veto Balint
2002-02-21
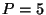
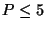
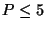 és
és 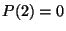
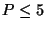 és
és 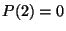 vagy
vagy 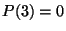
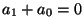 , ahol
, ahol 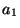 az elsőfokú tag együtthatója,
az elsőfokú tag együtthatója, 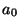 pedig a konstans
tag
pedig a konstans
tag
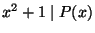
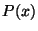 -nek van valós gyöke
-nek van valós gyöke
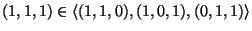
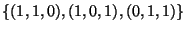 vektorok generátorrendszert alkotnak.
vektorok generátorrendszert alkotnak.
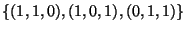 vektorok lineárisan függetlenek.
vektorok lineárisan függetlenek.
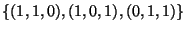 vektorok bázist (lineárisan független
generátorrendszert) alkotnak.
vektorok bázist (lineárisan független
generátorrendszert) alkotnak.
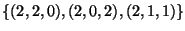 vektorok generátorrendszert alkotnak.
vektorok generátorrendszert alkotnak.
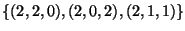 vektorok lineárisan függetlenek.
vektorok lineárisan függetlenek.
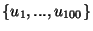 lineárisan független és
lineárisan független és
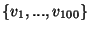 is
lineárisan független, akkor
is
lineárisan független, akkor
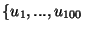 ,
,
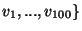 is
lineárisan független.
is
lineárisan független.
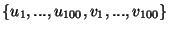 lineárisan független, akkor
lineárisan független, akkor
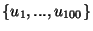 és
és
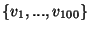 is lineárisan független.
is lineárisan független.
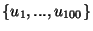 lineárisan független és
lineárisan független és
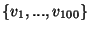 is
lineárisan független, akkor
is
lineárisan független, akkor 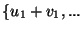 ,
,
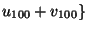 is lineárisan
független.
is lineárisan
független.
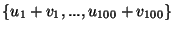 lineárisan független, akkor
lineárisan független, akkor
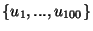 és
és
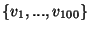 is lineárisan független.
is lineárisan független.
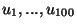 közül bármely 99 vektor lineárisan független,
akkor
közül bármely 99 vektor lineárisan független,
akkor
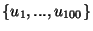 is lineárisan független.
is lineárisan független.
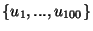 lineárisan független, akkor
lineárisan független, akkor
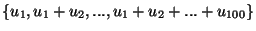 is lineárisan független.
is lineárisan független.
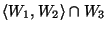 és
és
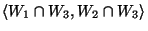 ;
;
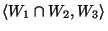 és
és
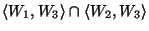 ;
;
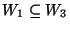 esetén
esetén
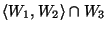 és
és
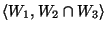 ?
?