Formális nyelvek gyakorlat (7)
2005. november 3., csütörtök
1. PDA kell ahhoz a nyelvhez, melynek ábécéje az 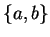 és szavaiban az
és szavaiban az 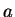 és
a
és
a 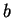 karakterek száma megegyezik.
karakterek száma megegyezik.
2. Automata kell (első kérdés, hogy milyen?):
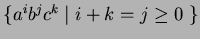
3. Determinisztikus PDA kell a következő nyelvhez:
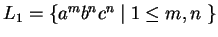
4. Az 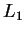 és az
és az 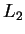 nyelveket is az definiálja, hogy bennük az
nyelveket is az definiálja, hogy bennük az 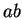 és a
és a 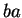 minirészsorozatok száma azonos. Viszont
minirészsorozatok száma azonos. Viszont 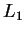 ábécéje az
ábécéje az 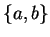 ,
, 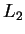 -é
pedig az
-é
pedig az 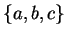 . Mindkét nyelvre kell automata vagy nyelvtan.
. Mindkét nyelvre kell automata vagy nyelvtan.
5. PDA kell a következő nyelvhez:
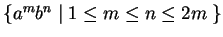
6. Tervezzen automatát azon
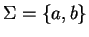 feletti nyelvhez,
melynek szavaiban a magányos b-k száma meghaladja az egynél hosszabb
homogén a sorozatok számát.
feletti nyelvhez,
melynek szavaiban a magányos b-k száma meghaladja az egynél hosszabb
homogén a sorozatok számát.
7. A kétirányú PDA, olyan mint a sima PDA, csak bír visszafele is menni.
(Ahogy a 2VA-nál volt.) Akkor fogad el, ha végigolvassa a szót és elfogadó
állapotba kerül. Kérdés: erősebb-e ez, mint a sima PDA?
(Segítség: az 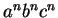 nyelv nem CF nyelv.)
nyelv nem CF nyelv.)
8. (a)
Adj veremautomatát az
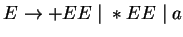 nyelvtanhoz az órán tanult
első konstrukcióval (ami nem röntgenszemű PDA-t ad).
nyelvtanhoz az órán tanult
első konstrukcióval (ami nem röntgenszemű PDA-t ad).
(b) Adj egy elfogadó lépéssorozatot a 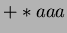 szóhoz a PDA-ban!
Adj egy nem elfogadót is! Hogy működik a PDA a
szóhoz a PDA-ban!
Adj egy nem elfogadót is! Hogy működik a PDA a 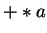 szón?
szón?
9. Környezetfüggetlen-e az alábbi nyelv?
(Ha igen, akkor adj PDA-t hozzá, ha nem, akkor bizonyítsd be ezt!)
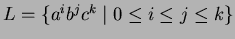
10. Igazak-e az alábbi állítások?
Az indoklás nem elhanyagolható része a válasznak.
- Minden többállapotú PDA-hoz létezik vele egyenértékű egyállapotú PDA.
- Egy reguláris nyelv minden részhalmaza reguláris.
- Ha az
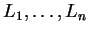 nyelvek (
nyelvek (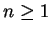 ) regulárisak, akkor az
) regulárisak, akkor az
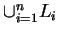 nyelv is reguláris.
nyelv is reguláris.
- Megszámlálhatóan végtelen sok reguláris nyelv uniója nem feltétlenül
reguláris
- Megszámlálhatóan végtelen sok reguláris nyelv uniója lehet
reguláris
- Attól. hogy
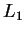 és
és 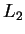 nem reguláris,
nem reguláris, 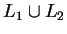 még lehet reguláris
még lehet reguláris
-