|
A pót zh egy jó megoldása
1. Az alábbi automata jó lesz:
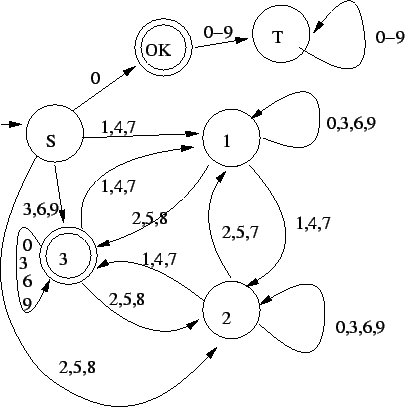
Az állapotok jelentései, ebből adódik, hogy mért jó az automata:
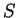 : még nem olvastunk semmit : még nem olvastunk semmit
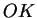 : nulla a szám eleje, az egy nulla az jó : nulla a szám eleje, az egy nulla az jó
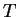 nulla után jön még más is, azaz biztos elutasítunk nulla után jön még más is, azaz biztos elutasítunk
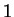 : az eddigi maradék 1 : az eddigi maradék 1
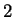 : az eddigi maradék 2 : az eddigi maradék 2
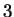 : az eddigi maradék 0 : az eddigi maradék 0
Itt végülis azt nézzük az állapotokban, hogy az eddig beolvasott szám mennyi
maradékot ad 3-mal osztva.
A következő számjegy beolvasásakor egyszerűen csak össze
kell adni az eddigi maradékot a számmal, ami jött és mod 3 nézni az eredményt.
Ez minimális lesz, mert
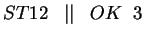
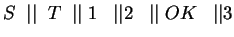 Azaz egy lépésben szétesnek az osztályok.
Azaz egy lépésben szétesnek az osztályok.
2. Az órán tanult algoritmus szerint eljárva:
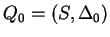 , ahol , ahol
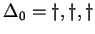
(A falaknál a visszatérő állapotokat 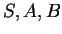 sorrendben sorolom fel, tehát
az első helyen áll az sorrendben sorolom fel, tehát
az első helyen áll az 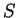 -hez, aztán az -hez, aztán az 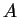 -hoz, végül pedig a -hoz, végül pedig a 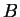 -hez
tartozó visszatérő állapot.) -hez
tartozó visszatérő állapot.)
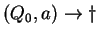
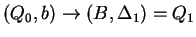 , ahol , ahol
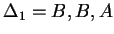
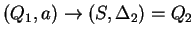 , ahol , ahol
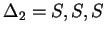
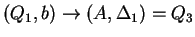
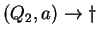
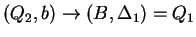
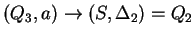
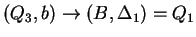
Tehát az egyirányú automata, ami determinisztikus és egy kezdőállapotú:
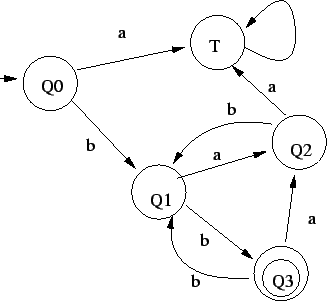
3. Először felrajzoljuk a nyelvtanból az automatát:
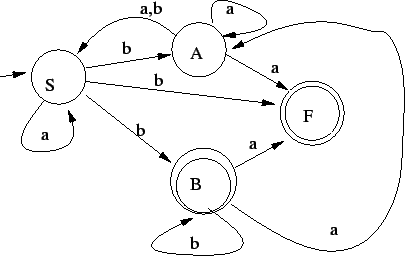
Ezt determinizáljuk és teljesen specifikáljuk:
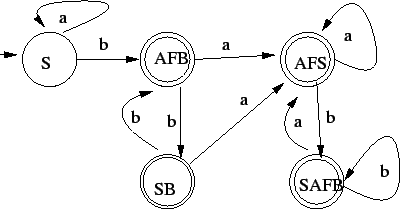
Ezt még minimalizáljuk, mivel minimálautomata kell. Észrevesszük, hogy
az összes elfogadó állapot egybevonható, mivel ezekből soha nem térünk
vissza S-be:
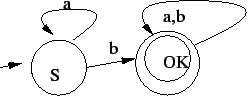
Ennek komplementerét véve:
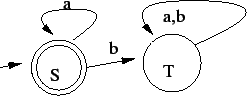
A reguláris kifejezés innen adódik: 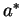 . .
4.
Egy jó automata:
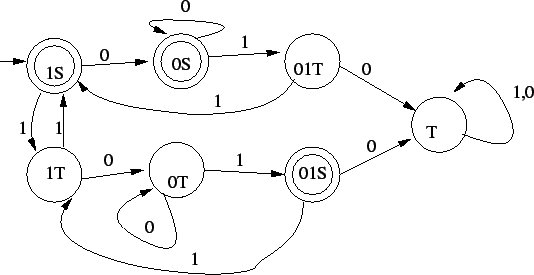
Magyarázat ehhez:
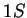 -ben vagyunk, ha páros sok -ben vagyunk, ha páros sok 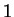 jött eddig és utoljára se jött eddig és utoljára se 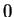 -t, se -t, se
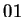 -t nem olvastunk és -t nem olvastunk és 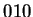 még nem volt még nem volt
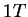 -ben vagyunk, ha páratlan sok -ben vagyunk, ha páratlan sok 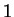 jött eddig és utoljára se jött eddig és utoljára se 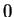 -t, se -t, se
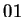 -t nem olvastunk és -t nem olvastunk és 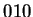 még nem volt még nem volt
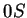 -ben vagyunk, ha páros sok -ben vagyunk, ha páros sok 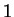 jött eddig és utoljára jött eddig és utoljára 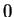 -t olvastunk
és -t olvastunk
és 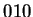 még nem volt még nem volt
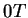 -ben vagyunk, ha páratlan sok -ben vagyunk, ha páratlan sok 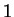 jött eddig és utoljára jött eddig és utoljára 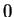 -t olvastunk
és -t olvastunk
és 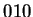 még nem volt még nem volt
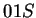 -ben vagyunk, ha páros sok -ben vagyunk, ha páros sok 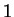 jött eddig és utoljára jött eddig és utoljára 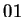 -t olvastunk
és -t olvastunk
és 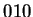 még nem volt még nem volt
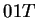 -ben vagyunk, ha páratlan sok -ben vagyunk, ha páratlan sok 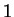 jött eddig és utoljára jött eddig és utoljára 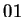 -t olvastunk
és -t olvastunk
és 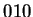 még nem volt még nem volt
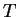 -ben vagyunk, ha volt már -ben vagyunk, ha volt már 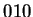
A reguláris kifejezés egyenletek felírásával:
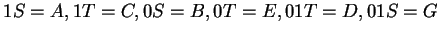 átírással és a csapda lehagyásával: átírással és a csapda lehagyásával:
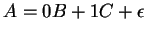
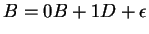
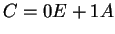
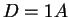
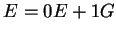
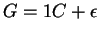
Innen:
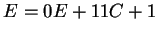 , majd , majd 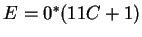
illetve
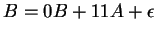 , majd , majd
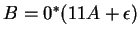
Az elsőt a 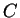 -s egyenletbe beírva: -s egyenletbe beírva:
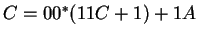 , azaz , azaz
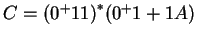 . .
Ezt és a második egyenletet az 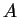 -s eredeti egyenletbe visszaírva: -s eredeti egyenletbe visszaírva:
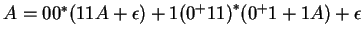 , ahonnan , ahonnan
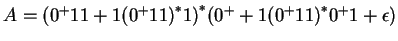
5. Az 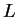 nyelv nem reguláris, ezt a pumpálási lemmával igazoljuk.
Ha nyelv nem reguláris, ezt a pumpálási lemmával igazoljuk.
Ha 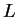 reguláris lenne, akkor létezne egy olyan reguláris lenne, akkor létezne egy olyan 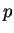 szám, ami a lemmában
van. Vegyün ezen szám, ami a lemmában
van. Vegyün ezen 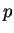 -vel az -vel az 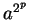 szót. Ez a szó szót. Ez a szó 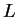 -ben van és
hosszabb -ben van és
hosszabb 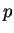 -nél. Jelöljük ki benne az -nél. Jelöljük ki benne az 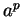 kezdőszeletet, vagyis az
első kezdőszeletet, vagyis az
első 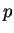 a-betűt. Mivel ez sem rövidebb a-betűt. Mivel ez sem rövidebb
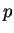 -nél, a lemma miatt ebben kell tudnunk találni egy olyan részszót, melyet
lehet ismételgetni úgy, hogy még mindig a nyelvben maradunk.
De ha itt pumpálunk, akkor az első pumpálásnál, amikor kétszer ismétlejük meg
a pumpálandó részszót a szó hossza -nél, a lemma miatt ebben kell tudnunk találni egy olyan részszót, melyet
lehet ismételgetni úgy, hogy még mindig a nyelvben maradunk.
De ha itt pumpálunk, akkor az első pumpálásnál, amikor kétszer ismétlejük meg
a pumpálandó részszót a szó hossza 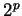 és és 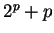 között lesz. Ez a hossz
biztosan nem kettô-hatvány, vagyis kikerültünk a nylevből, mégsem lehet
pumpálni. között lesz. Ez a hossz
biztosan nem kettô-hatvány, vagyis kikerültünk a nylevből, mégsem lehet
pumpálni.
|






