|
Pumpálási lemma reguláris nyelvekre
Állítás (Ez a lemma állítása)
Ha 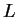 reguláris nyelv, akkor reguláris nyelv, akkor
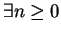 egész szám, hogy egész szám, hogy
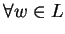 , ahol , ahol 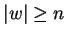 és
w minden és
w minden
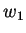 részszavára,
ahol
részszavára,
ahol
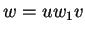 és és 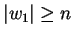 , létezik , létezik 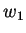 -nek egy -nek egy 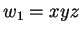 felosztása,
amelyben felosztása,
amelyben
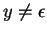 és amely felbontásra és amely felbontásra 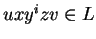 minden minden
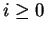 esetén. esetén.
Azaz: Ha 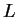 egy reguláris nyelv, akkor létezik egy olyan hossz, aminél
hosszabb tetszőleges egy reguláris nyelv, akkor létezik egy olyan hossz, aminél
hosszabb tetszőleges 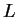 -beli szóban tetszőlegesen kiválasztva egy ennél a hossznál
nagyobb részszót igaz lesz a következő:
ezen részszóban van egy olyan rész valahol,
melyet tetszőlegesen sokszor megismételve (vagy elhagyva) még mindig -beli szóban tetszőlegesen kiválasztva egy ennél a hossznál
nagyobb részszót igaz lesz a következő:
ezen részszóban van egy olyan rész valahol,
melyet tetszőlegesen sokszor megismételve (vagy elhagyva) még mindig 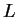 -beli
szavakat kapunk. -beli
szavakat kapunk.
Ennek a haszna:
Segítségével be lehet látni nyelvekről, hogy nem regulárisak.
Ez úgy megy, hogy ha megmutatjuk egy nyelvről, hogy van olyan szava,
amiben nem lehet a fentiek szerint pumpálni, akkor az tuti nem reguláris.
Vigyázat! Lehetnek olyan nyelvek, amiket lehet pumpálni, de mégsem regulárisak.
Vagyis ez a lemma csak a nem-reguláris nyelvek egy részét buktatja le.
Például az
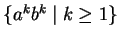 nyelv nem reguláris, mert: nyelv nem reguláris, mert:
Tegyük fel, hogy az.
Vegyük az 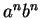 szót, ahol az szót, ahol az 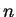 az az az az 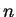 , aminek létezését a
lemma garantálja és jelöljük ki , aminek létezését a
lemma garantálja és jelöljük ki 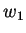 -nek az -nek az 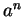 részszót!
Ha ebben pumpálunk, akkor az részszót!
Ha ebben pumpálunk, akkor az 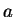 -k száma megnő, de közben a -k száma megnő, de közben a 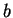 -k száma
nem változik, azaz a kapott szó nem lesz eleme a nyelvnek. -k száma
nem változik, azaz a kapott szó nem lesz eleme a nyelvnek.
Ezzel beláttuk, hogy a nyelv nem reguláris.
A lemma bizonyítása:
Ha az 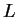 nyelv reguláris, akkor van egy olyan véges automata, ami
elfogadja őt. Legyen nyelv reguláris, akkor van egy olyan véges automata, ami
elfogadja őt. Legyen 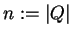 , azaz , azaz 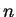 legyen az automata állapotainak
a száma.
Nézzük, hogy az automata milyen állapotokat érint,
onnantól kezdve, hogy rálép a legyen az automata állapotainak
a száma.
Nézzük, hogy az automata milyen állapotokat érint,
onnantól kezdve, hogy rálép a
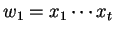 ( (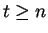 ) szó első
betűjére, egészen odáig, hogy lelép az utolsóról is.
Ez összesen ) szó első
betűjére, egészen odáig, hogy lelép az utolsóról is.
Ez összesen 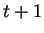 állapot: állapot:
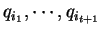 .
Mivel ez több, mint amennyi állapota az automatának van, biztosan van
közöttük két egyforma. Ha .
Mivel ez több, mint amennyi állapota az automatának van, biztosan van
közöttük két egyforma. Ha
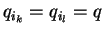 , akkor ez éppen azt jelenti, hogy
a szó olvasása során az automata az , akkor ez éppen azt jelenti, hogy
a szó olvasása során az automata az
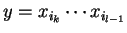 részszó
olvasását a részszó
olvasását a 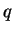 állapotban kezdi el, elolvassa részszót és
ekkor is állapotban kezdi el, elolvassa részszót és
ekkor is 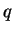 -ban van.
Ha ekkor megint az -ban van.
Ha ekkor megint az 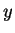 részszó jönne (akárhányszor),
akkor megint csak részszó jönne (akárhányszor),
akkor megint csak 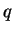 -ba kerülne. Mivel az eredeti teljes -ba kerülne. Mivel az eredeti teljes 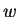 szó elolvasása
után elfogadóban áll meg az automata (azaz a szó elolvasása
után elfogadóban áll meg az automata (azaz a 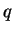 -ból tovább
olvasva a maradék szót
elfogadóba jutunk), a sok -ból tovább
olvasva a maradék szót
elfogadóba jutunk), a sok 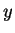 -t tartalmazó futásokkor is
lesz vele, azaz ezeket a szavakat is elfogadja. -t tartalmazó futásokkor is
lesz vele, azaz ezeket a szavakat is elfogadja.
Az 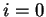 eset úgy jön ki, hogy ha kihagyjuk az eredeti szóból az eset úgy jön ki, hogy ha kihagyjuk az eredeti szóból az 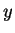 -t,
a maradék szót akkor is
a -t,
a maradék szót akkor is
a 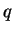 állapotból kezdjük el elolvasni, úgy meg elfogadunk. állapotból kezdjük el elolvasni, úgy meg elfogadunk.
|