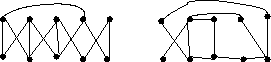Bevezetés a számításelméletbe II.
2002. február 21.
1. Egy  gráfról csak annyit tudunk, hogy fokszámai: 2,3,3,3,3,4.
Mutasd meg, hogy biztosan van Hamilton-kör a gráfban!
gráfról csak annyit tudunk, hogy fokszámai: 2,3,3,3,3,4.
Mutasd meg, hogy biztosan van Hamilton-kör a gráfban!
2. Egy  gráfról csak annyit tudunk, hogy fokszámai: 2,3,3,4,4,5,5
Mutasd meg, hogy biztosan van Hamilton-kör a gráfban!
gráfról csak annyit tudunk, hogy fokszámai: 2,3,3,4,4,5,5
Mutasd meg, hogy biztosan van Hamilton-kör a gráfban!
3. Páros gráf-e a 6, illetve 5 hosszúságú kör? És egy tetszőleges fa?
4. Van-e teljes párosítás az alábbi gráfban?
5.
Létezik-e olyan 6 pontú és 11 ill. 12 élű egyszerű gráf, amelynek
nincs Hamilton-köre?
6. Melyik gráf páros?
7. Legyen  egy egyszeru, összefüggo, páros gráf,
amelynek mindkét
pontosztályában
egy egyszeru, összefüggo, páros gráf,
amelynek mindkét
pontosztályában 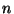 pont van. Az egyik osztályban minden pont foka
különbözo. Bizonyítsuk be, hogy
pont van. Az egyik osztályban minden pont foka
különbözo. Bizonyítsuk be, hogy 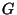 -ben van teljes
párosítás!
-ben van teljes
párosítás!
8. HF!!!! ZH! Egy 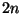 pontú gráf minden pontjának a foka legalább
pontú gráf minden pontjának a foka legalább
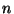 . Bizonyítsuk be, hogy ekkor van benne teljes párosítás.
. Bizonyítsuk be, hogy ekkor van benne teljes párosítás.
9. HF!!!! A 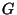 összefüggő gráf tetszőleges pontját elhagyva a
kapott gráfnak létezik teljes párosítása. Bizonyítsuk be, hogy a
összefüggő gráf tetszőleges pontját elhagyva a
kapott gráfnak létezik teljes párosítása. Bizonyítsuk be, hogy a
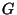 gráfban nincs elvágó él, vagyis tetszőleges élet elhagyva a gráf továbbra is összefüggő marad.
gráfban nincs elvágó él, vagyis tetszőleges élet elhagyva a gráf továbbra is összefüggő marad.
10. HF!!!! ZH! Egy 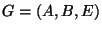 páros gráfban teljesül az, hogy
páros gráfban teljesül az, hogy 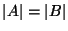 és minden
és minden
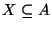 valódi részhalmazra
valódi részhalmazra
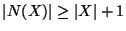 . Bizonyítsuk be, hogy a gráf
minden
. Bizonyítsuk be, hogy a gráf
minden 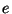 éléhez van
éléhez van 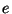 -t tartalmazó teljes párosítás.
-t tartalmazó teljes párosítás.
11. Egy kiránduláson 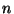 házaspár vesz részt, és közöttük
kellene elosztani
házaspár vesz részt, és közöttük
kellene elosztani 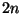 különbözo csokoládét úgy, hogy mindenki
egyet kapjon. Tudjuk, hogy minden résztvevo legalább
különbözo csokoládét úgy, hogy mindenki
egyet kapjon. Tudjuk, hogy minden résztvevo legalább 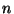 fajtát
szeret a
fajtát
szeret a 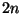 csokoládé közül, és az is teljesül, hogy minden
csokoládét szereti minden házaspárnak legalább az egyik
tagja. Bizonyítsuk be, hogy ekkor kioszthatók úgy a csokoládék,
hogy mindenki olyat kapjon, amit szeret.
csokoládé közül, és az is teljesül, hogy minden
csokoládét szereti minden házaspárnak legalább az egyik
tagja. Bizonyítsuk be, hogy ekkor kioszthatók úgy a csokoládék,
hogy mindenki olyat kapjon, amit szeret.
12. (a) Igaz-e, hogy ha egy páros gráfban van Hamilton-kör, akkor teljes
párosítást is tartalmaz?
(b) Igaz-e ez fordítva? (Ha van teljes párosítás egy páros gráfban, akkor
létezik-e Hamilton kör?)
(c) (a) Igaz-e, hogy ha egy (nem feltétlenül páros)
gráfban van Hamilton-kör, akkor teljes párosítás is van?
13. (a) Mutassuk meg, hogy egy 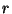 -reguláris páros gráf biztosan
teljesíti a Hall-feltételt!
-reguláris páros gráf biztosan
teljesíti a Hall-feltételt!
(b) Egy páros gráf minden csúcsába pontosan 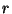 él fut.
Véletlenül éppen
él fut.
Véletlenül éppen 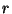 darab különbözo színu ceruzánk van
(a feketén kívül, amivel az eredeti ábra készült).
Bizonyítsuk be, hogy az élek kihúzhatók színessel
úgy, hogy minden csúcsba csupa különbözo
színu
menjen!
darab különbözo színu ceruzánk van
(a feketén kívül, amivel az eredeti ábra készült).
Bizonyítsuk be, hogy az élek kihúzhatók színessel
úgy, hogy minden csúcsba csupa különbözo
színu
menjen!
14. ZH! Legyen 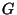 egy 3-reguláris, Hamilton-kört tartalmazó egyszerű gráf.
Bizonyítsuk be, hogy
egy 3-reguláris, Hamilton-kört tartalmazó egyszerű gráf.
Bizonyítsuk be, hogy 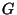 élhalmaza előáll 3 diszjunkt teljes párosítás
uniójaként!
élhalmaza előáll 3 diszjunkt teljes párosítás
uniójaként!
15. * Egy szigeten 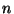 család él, mindegyik földet művel és
vadászik is. A Vadászat Istene felosztotta a szigetet
valahogy
család él, mindegyik földet művel és
vadászik is. A Vadászat Istene felosztotta a szigetet
valahogy 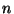 egyenlő területű részre, a Földművesség Istene
más szempontok alapján, másképp, szintén
egyenlő területű részre, a Földművesség Istene
más szempontok alapján, másképp, szintén 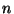 egyenlő területű részre. Mutassuk meg, hogy kaphat minden család mindkét fajta részből úgy egyet-egyet, hogy a két rész metszete ne legyen üres.
egyenlő területű részre. Mutassuk meg, hogy kaphat minden család mindkét fajta részből úgy egyet-egyet, hogy a két rész metszete ne legyen üres.
16. * Mutassuk meg, hogy ha egy gráfban létezik két teljes
párosítás, akkor létezik páros hosszú kör is!
17. * Legyen 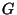 egy olyan síkbarajzolható, egyszerű gráf, ami tartalmaz
Euler-kört. Mutassuk meg, hogy
egy olyan síkbarajzolható, egyszerű gráf, ami tartalmaz
Euler-kört. Mutassuk meg, hogy 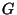 duálisa páros gráf!
duálisa páros gráf!
Csima Judit
2002-02-21