Bevezetés a számításelméletbe II.
2002. február 14.
1. Milyen 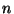 esetén tartalmaz az
esetén tartalmaz az 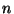 pontú teljes gráf
Euler kört, Euler utat, Hamilton kört és Hamilton utat?
pontú teljes gráf
Euler kört, Euler utat, Hamilton kört és Hamilton utat?
2. Egy oktaéder minden lapjára egy-egy azonos alapméretu
tetraédert illesztünk. Van-e az így keletkezett test
éleibol álló gráfban Hamilton-út?
3. A 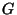 gráf pontjai egy 8-elemu halmaz 2-elemu
részhalmazainak felelnek meg. Két pont akkor van összekötve
egy éllel, ha a pontoknak megfelelo két részhalmaz
diszjunkt. Van-e
gráf pontjai egy 8-elemu halmaz 2-elemu
részhalmazainak felelnek meg. Két pont akkor van összekötve
egy éllel, ha a pontoknak megfelelo két részhalmaz
diszjunkt. Van-e 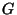 -ben Hamilton-kör? És Hamilton út?
-ben Hamilton-kör? És Hamilton út?
4. ZH!
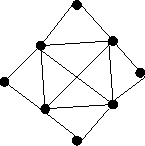
Hányszor kell minimálisan felemelni a ceruzát az alábbi gráf lerajzolásához?
(Egy élet csak egyszer rajzolhatunk meg.)
5. Milyen 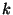 és
és 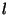 értékekre tartalmaz Hamilton-kört, ill. utat
a
értékekre tartalmaz Hamilton-kört, ill. utat
a 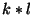 pontból álló rács?
pontból álló rács?
6.
Egy 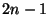 pontú gráf minden pontjának a foka legalább
pontú gráf minden pontjának a foka legalább
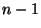 . Bizonyítsuk be, hogy ekkor létezik a gráfban Hamilton-út!
. Bizonyítsuk be, hogy ekkor létezik a gráfban Hamilton-út!
7. HF!!!!
Hogyan változhat egy gráfban a Hamilton-kör megléte,
ha behúzunk illetve törlünk egy élt? Az Euler-körről tudunk valami ilyet állítani?
8. HF!!!! Egy 2000 csúcsú 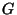 gráfban a minimális fokszám 1500. Biz.be, hogy
gráfban a minimális fokszám 1500. Biz.be, hogy 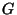 tartalmaz legalább 251 páronként éldiszjunkt Hamilton-kört!
tartalmaz legalább 251 páronként éldiszjunkt Hamilton-kört!
9. HF!!!! Bizonyítsuk be, hogy minden 8-reguláris gráfból el lehet hagyni éleket
úgy, hogy minden csúcs foka pontosan 4 legyen.
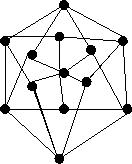
10. (a) Legalább hány élet kell hozzávenni az alábbi gráfhoz, hogy legyen
benne Euler-kör?
(b) Legalább hány élet kell kitörölni az alábbi gráfból, hogy legyen
benne Euler-kör?
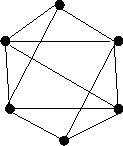
11. Van-e Hamilton kör az alábbi gráfban?
12. A 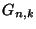 gráf pontjai egy
gráf pontjai egy 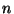 elemű halmaz
elemű halmaz 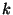 elemű részhalmazainak
felelnek meg. Két pont akkor van összekötve, ha a nekik megfelelő részhalmazok
diszjunktak. Van-e Euler- illetve Hamilton-köre a
elemű részhalmazainak
felelnek meg. Két pont akkor van összekötve, ha a nekik megfelelő részhalmazok
diszjunktak. Van-e Euler- illetve Hamilton-köre a 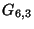 -nak és a
-nak és a
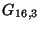 -nak?
-nak?
13. * Mutassuk meg, hogy egy összefüggő gráf élei bejárhatók úgy, hogy
mindegyiken pontosan kétszer megyünk végig, mégpedig mindkét irányban egyszer!
14. *, ZH!
Az 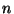 pontú egyszerű
pontú egyszerű 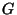 gráfban minden olyan
gráfban minden olyan 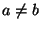 csúcspárra,
melyek nincsenek éllel összekötve teljesül az, hogy
csúcspárra,
melyek nincsenek éllel összekötve teljesül az, hogy
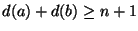 .
Igazoljuk, hogy
.
Igazoljuk, hogy 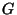 minden
minden 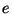 éléhez van
éléhez van 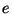 -n átmenő Hamilton kör!
-n átmenő Hamilton kör!
15. *, ZH!
Egy 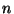 tagú társaságban bármely három ember között van kettő,
aki nem ismeri egymást.Tudjuk azt is, hogy a társaságban mindenki legalább
tagú társaságban bármely három ember között van kettő,
aki nem ismeri egymást.Tudjuk azt is, hogy a társaságban mindenki legalább
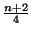 embert ismer (az ismeretségek kölcsönösek).
Bizonyítsuk be, hogy a társaság tagjai leültethetők egy kerek asztal
mellé úgy, hogy a szomszédos emberek vagy ismerik egymást vagy van közös
ismerősük.
embert ismer (az ismeretségek kölcsönösek).
Bizonyítsuk be, hogy a társaság tagjai leültethetők egy kerek asztal
mellé úgy, hogy a szomszédos emberek vagy ismerik egymást vagy van közös
ismerősük.
Csima Judit
2002-02-14