Önálló labor feladatom volt egy ragelemző szoftver készítése. A program egy szólista alapján ismerje fel a ragcsoportokat, és javasoljon további olyan értelmes szavakat, amik az eredeti listában nincsenek benne. A program tehát nem rendelkezik a nyelvről semmilyen információval, pusztán egy szóhalmaz áll rendelkezésére.
Tudván, hogy a nyelv ragozó, találja meg a ragcsoportokat, és azokat a szavakat, amelyek nem minden ragozott alakja található meg a szóhalmazban. Ezután javasolja ezen szavak megfelelően ragozott alakjának felvételét. Ezáltal a szóhalmaz teljes lesz, abban az értelemben, hogy ha van egy szó, ami néhány raggal szerepel, akkor a szóhoz kapcsolható összes raggal szerepelni fog.
Az így előállított szóhalmazt a program olyan struktúrában tárolja, ami egyrészt kis helyet foglal, másrészt gyorsan lehet vele műveleteket végezni. Ez a struktúra már alapjául szolgálhat helyesírás ellenőrző szoftver készítéséhez.
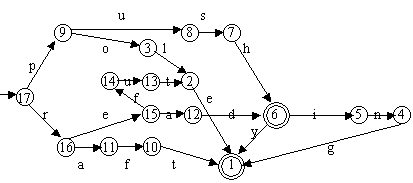
A program a szavakat egy speciális végesautomatában tárolja. A végesautomata egy olyan irányított gráf, amely pontjai állapotoknak felelnek meg, élei pedig betűket reprezentálnak. Az állapotok között van egy kitüntetett, az úgynevezett kezdőállapot, továbbá minden állapot vagy elfogadó, vagy elutasító állapot.
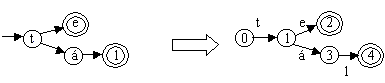
Egy végesautomata akkor fogad el egy szót, ha a kiindulási állapotból indulva, a szónak megfelelő úton haladva, a végállapot elfogadó állapot lesz. A szónak megfelelő út azt jelenti, hogy az i-edik lépésnél azon élen haladunk tovább, amelyik élhez tartozó betű a szó i-edik betűjével egyezik meg. Nyilván akkor jutunk a végállapotba, ha a lépések során, a szó végére értünk. Az alábbi ábrán egy végesautomata látható, ahol az elfogadó állapotokat dupla körrel ábrázoltam:

A feladat tehát, azokat a nevezetes állapotokat megtalálni, amelyek nyelv nevezetes ragcsoportjait reprezentálják. Ha ez megvan, akkor olyan állapotokat kell keresni, amik ezen ragcsoportok alapján kicsit hiányosak, azaz kevés kivétellel tartalmazzák a nevezetes ragcsoport ragjait. Ha a hiányzó ragokat az állapot által reprezentált szótövekhez hozzáfűzzük, akkor értelmes szót kell kapjak. Látni kell, hogy azokkal az extra ragokkal, amik a vizsgált állapothoz igen, viszont a nevezetes állapotokhoz nem csatlakozik, nem kell foglalkozni, hiszen olyan szavak minden nyelvben előfordulnak, amelyek valamilyen másik értelmes szó meghosszabbítása. A nevezetes állapotokhoz tartozó ragok halmazait hívjuk ezentúl fő ragcsoportoknak. Az egész algoritmus egy sarkalatos pontja ezek a ragcsoportok megtalálása. Mivel egy fő ragcsoport sok szótőhöz csatlakozik, továbbá a ragcsoportban található ragok száma ne legyen kicsi (könnyű átgondolni, hogy kevés ragú ragcsoportokkal mért nem tudunk algoritmikus eszközökkel semmit sem kezdeni), ezért azokat az állapotokat tekintem nevezetes állapotoknak, ahol a (szótőszámi * ragszámj) szorzat nagy. A szorzatban szereplő i, j a nyelvre jellemző konstansok, amelyek alapértelmezése 1. Ha még olyan kényszereket is meghatározunk, hogy legalább hány szótő illetve rag tartozzon a fő ragcsoportokhoz, akkor az állapotok között egy sorrendet állíthatunk fel. A hiányos állapotokat ezekkel az állapotokkal fogjuk összehasonlítani.
Abban az esetben, ha egy javasolt szót elfogadunk, mert értelmes, akkor módosítanunk kell a végesautomatát. Sajnos nem ismert olyan algoritmikus módszer, ami egy minimálautomatából új szó hozzáadásával új minimálautomatát generál. Ezért az egyetlen megoldás, hogy az új szót felvesszük a szófába, és újra generáljuk a végesautomatát.
A végesautomata nagy elemszámú szóhalmazt jól tömörítve tárol, továbbá gyorsan lehet vele műveleteket végezni. Például, hogy egy szót tartalmaz-e a szóhalmazt reprezentáló végesautomata, el lehet dönteni maximum (szóhossz * nyelv betűinek száma) feltétel kiértékelésével. Egy rendezett szövegfájlban ez log(n) lenne, ahol n a szavak száma. Hasonlóan a ragok és szótövek megkeresése is rendkívül gyorsan megvalósítható.
A program Windows 9x környezetben futtatható.
Miután elindítottuk a programot, meg kell adnunk a fájl nevét, ami a szavakat tartalmazza. A program feltételezi, hogy sima szöveges fájlról van szó, továbbá egy sorban egy szó található. A sorban minden karaktert a szó betűjeként értelmez.
A program ezután felépíti a szófát, majd abból a végesautomatát. Ez, a szavak számának függvényében, akár perceket is igénybe vehet. A végesautomata alapján listát ad a fő ragcsoportokról. A lista eső tagjának legnagyobb a (szótőszámi * ragszámj) szorzata. A fő ragcsoportok kiválasztásának paramétereit a settings menüpontban lehet beállítani.
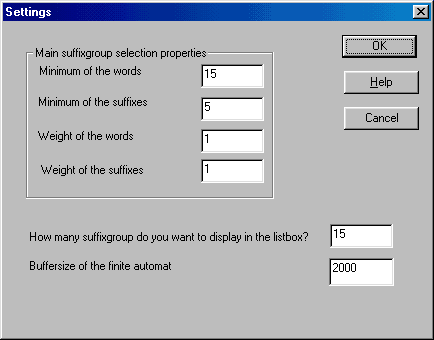
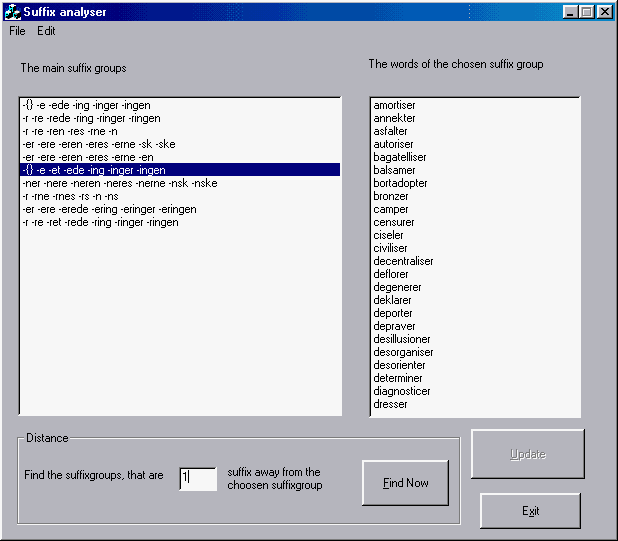
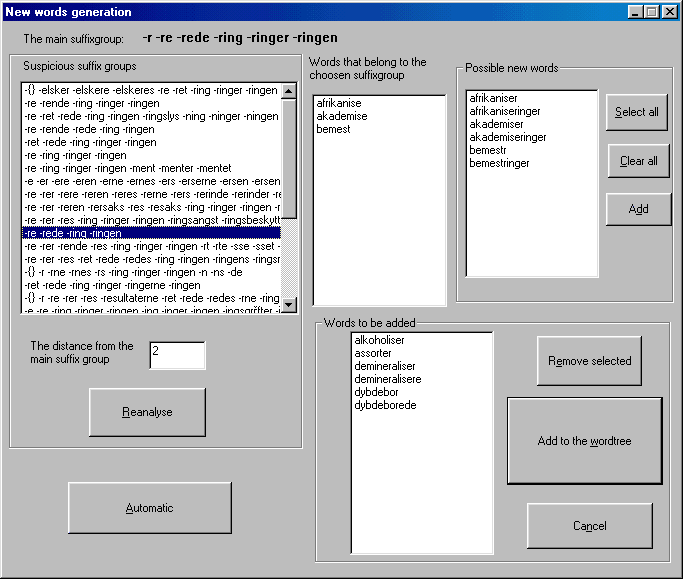
Ha megnyomjuk az Add to the wordtree gombot, akkor az ablak bezárul, visszatérünk az előző ablakhoz, és a szófát bővítjük az új szavakkal. Új végesautomatát azonban nem generálunk. Ezt az Update gomb megnyomásával érhetjük el. A két lépés különválasztásának az oka az, hogy a végesautomata generálása sok időbe telik. Célszerű ezért először összegyűjteni az új szavakat, majd egyszer újragenerálni a szófát. Tehát a program hatékony használatánál először végignézzük a fő ragcsoportokat, kiválasztjuk mindegyikhez az új, értelmes szavakat, majd ha végeztünk minden ragcsoporttal, akkor generáljuk csak újra a végesautomatát, és vizsgáljuk az új lehetőségeket.
A végső célunk az, hogy az új szavakat az eredeti fájlba is beírjuk. Ezt a Save vagy a Save as menüpontokkal tehetjük meg. Alapból csak azokat a szavakat írja ki fájlba, amik felvétele után megnyomtuk az Update gombot, de ha vannak olyan szavak, amiket nem Updateltünk, akkor egy figyelmeztető üzenet kérdezi meg, hogy elvégezze-e ezt a műveletet.
Amennyiben ki akarunk lépni a programból, az Exit gombot kell megnyomni. Ekkor, ha vannak szavak, amiket még nem mentettünk el, akkor a program rákérdez, hogy megtegye-e ezt. Ha olyan szavak is vannak, amik felvétele után nem nyomtuk meg az Update gombot, akkor ezeket a szavakat is kiírhatjuk anélkül, hogy új végesautomatát generálnánk. Ez jogos igény, lévén mi ki akartunk lépni a programból, esetleg a szavak elmentésével, így már nincs szükségünk semmilyen automatára.
A program az új szavakat az eredeti szavak végére fűzi, minden sorba egyet (kivéve, ha a Save as menüponton keresztül új fájlt generálunk. Ilyenkor névsorba rendezett fájlt kapunk).
Ebben a részben szó lesz arról, hogy hogyan kell felépíteni a minimális automatát, hogyan kell azt bejárni a ragok és a szótövek megtalálásához. Ezenkívül szó lesz arról, a szófa és a végesautomata adatszerkezetéről, továbbá az osztályok függvényeiről.
Az építés során a szófa minden pontjának a végesautomata egy állapotát fogjuk megfeleltetni. Mivel a végesautomata a szófa egy tömörített változata, ezért nyilván lesznek olyan pontok, amelyek ugyanahhoz az állapothoz lesznek rendelve.
Kezdetben a végesautomata két állapotot, a végleges elfogadó, és a végleges elutasító állapotot tartalmazza. Ezekből az állapotokból semmilyen betű hatására nem juthatunk másik állapotba.
A szófából a végesautomata felépítése rekurzívan történik. Ahhoz, hogy egy ponthoz állapotot tudjunk rendelni, ismerni kell a belőle induló élek végpontjainak állapotait a végesautomatában. Ha ezeket tudjuk, akkor a pont állapotát jellemezni tudjuk, hiszen meg tudjuk mondani, hogy tetszőleges betű hatására milyen új állapotba kell jutni. Ez után végignézzük, hogy van-e már ilyen állapot az eddig felépített végesautomatánkban. Ha van, akkor ennek sorszáma lesz a pont állapota, ha nincs, akkor bővíteni kell a végesautomatát az új állapottal, és a pont állapotának ezt az új állapotot kell megfeleltetni.
Látható tehát, hogy egy pont állapotának meghatározásához, a szomszédjai állapotait kell tudni. A rekurzió akkor ér véget, ha levélbe jutunk (ahonnan nincs tovább él), hiszen a levél állapota nem más, mint a végleges elfogadó állapot.
Az algoritmus, nagy szófa esetében, meglehetősen időigényes. Ennek az oka, hogy mielőtt új állapotot veszünk fel, végig kell néznünk a végesautomatát, hogy az tartalmazza-e. Ehhez nyilván nem tehetünk mást, mint hogy összehasonlítjuk az automata összes állapotával. Két állapot összehasonlítása pedig, a belőle kiinduló összes él, és azok végpontjainak vizsgálatát igénylik. Ahogy nő a végesautomata, úgy vesz egy állapot beszúrása egyre több időt igénybe.
Egy gyorsítási lehetőség alapötlete az, hogy ha egy pont fiának állapota új volt, tehát még nem szerepelt azelőtt az automatában, akkor nyilván az eredeti állapot is csak új lehet, hisz olyan állapotra mutat, amire még nem mutathatott senki. Éppen ezért ezt az állapotot ne vizsgáljuk meg, hogy benne van-e az automatában, vagy sem, hanem egyszerűen szúrjuk a végére. A minimálautomata építése során, tehát célszerű tárolni, hogy egy adott pont állapota új, vagy sem. Ha egy pont fiai között van új, akkor ő is új lesz. Kiinduláskor minden levél állapota régi. Egy állapotot akkor nyilvánítunk réginek, ha egyrészt minden szomszédja régi, másrészt már található ilyen állapot a végesautomatában.
A fent leírt algoritmust nevezik gyorsított Frey algoritmusnak.
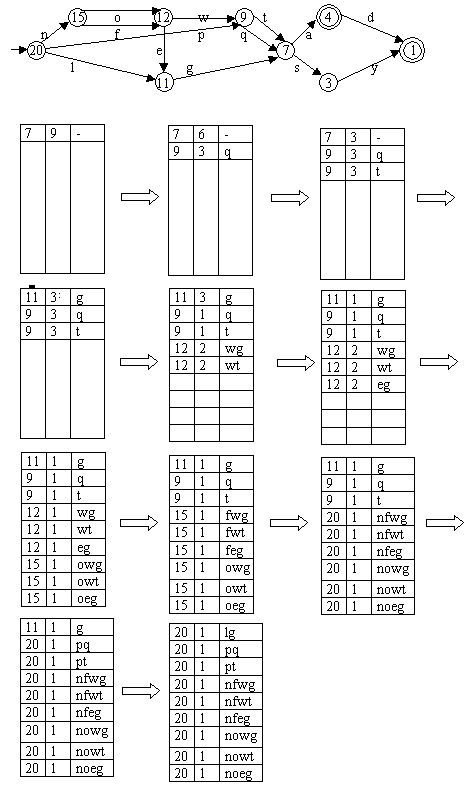
Az alábbi kép egy példát mutat szófa átalakítására minmálautomatává, gyorsított Frey algoritmussal.

A következő gyorsítási lehetőség azon a megfigyelésen alapul, hogy a természetes nyelvek szavaiból felépített szófa pontjainak 70-80%-a olyan pont, hogy csak egy él indul ki belőlük.
Célszerű tehát ezen pontok állapotainak sorszámát külön tárolni oly módon, hogy benne a keresés jóval gyorsabb legyen, mint a végesautomatánál. Ez könnyen megoldható 3 darab kétdimenziós tömb segítségével. Ha a végesautomatában van olyan "i" sorszámú állapot, amiből "c" betű hatására "j" sorszámú állapotba jut, akkor az első tömb "c" karakternek megfelelő sorában szerepelnie kell az "i" számnak, továbbá a második tömb ugyanezen pozíciójában "j" szám kell álljon, a harmadik tömb ezen pozíciójában pedig 1-es, ha "i" sorszámú állapot elfogadó, 0, ha nem.
Ha tehát a végesautomata építése során, olyan ponthoz jutunk, amiből csak egy él vezet "j" ponthoz, akkor nézzük meg, hogy van-e a második tömb, az élnek megfelelő sorában "j" sorszám. Ha van, és az is stimmel, hogy az állapot elfogadó vagy sem (amit a harmadik tömb alapján ellenőrizhetünk) akkor a pont állapota az első tömb megfelelő pozíciójában található sorszámú állapot. Ha nem található meg a "j" szám, akkor a végesautomatában nincs még ilyen állapot, tehát fel kell venni. Ilyenkor természetesen a három tömböt is bővíteni kell.
Ezzel a módszerrel a minimálautomata építése 4-5-ször gyorsabbá tehető.
Ebben a részben leírom, egy tetszőleges állapot ragjai, illetve szótövei megtalálására alkalmas alapalgoritmust. A következő részben, egy az alap szótőkeresési algoritmusnál jóval gyorsabb módszert mutatok be, és illusztrálom példával.
A ragkeresés nagyon egyszerű, lévén az állapot ragjait megkaphatjuk, ha a belőle induló él betűjét összefűzzük az él végállapotának ragjaival. Egy elfogadó állapot ragja az üres sztring. Amennyiben a nevezetes állapokat helyesen választjuk ki, akkor ez a ragkeresési algoritmus gyors lesz, annak ellenére, hogy rekurzív. Ez az állítás azért igaz, mert a fő ragcsoportokhoz közepes számú rag kapcsolódik, így a rekurzió nem lesz mély.
A szótőkeresési algoritmusok feltétele, hogy a végesautomata olyan legyen, hogy minden állapotból csak nála kisebb sorszámú állapotba mutat él. A Frey algoritmussal felépített automata ilyen tulajdonságú.
Az alapalgoritmus alapja ekkor az, hogy ha a kiinduló állapot fiai között van olyan állapot, amiből út vezet a nevezetes állapotba, akkor fiúra mutató él betűjének, és az utat reprezentáló élek karaktersorozatát összefűzve, egy szótövet kapunk. Azt, hogy a kiinduló állapot fiai között van-e út a nevezetes állapotba, hasonlóan vizsgáljuk, mint a kiinduló állapotba tennénk, tehát a fiúk fiait vesszük sorba. Mivel teljesül a fent említett feltétel, ezért, ha egy állapot fia kisebb sorszámú a nevezetes állapotnál, akkor azzal nem kell foglalkozni, lévén belőle nem vezethet út ebbe az állapotba. Ha egy állapotból él mutat a nevezetes állapotba, akkor az egy egy hosszú út.
Ez a módszer rekurzív, továbbá állapotok többszöri vizsgálatának lehetősége miatt lassú, és redundanciát tartalmaz.
A gyorsítás feltétele, hogy tudjuk minden állapotból, hány út vezet hozzá a kiindulási állapotból. Azt kell látni, hogy ezt a többletinformációt, a végesautomata, csökkenő sorrend szerinti egyszeri bejárásával, meg lehet szerezni. Ezt érdemes mindjárt az automata megépítése után megtenni, hiszen ez az információ nem csak itt, de a nevezetes állapot kiválasztásánál is szükséges.
A gyorsított algoritmusnál a kezdő állapot nem a kiinduló állapot, hanem az, amelyiknek a szótöveit keressük (tehát a nevezetes állapot). A végesautomatán egyesével haladunk növekvő sorszámú állapotokon keresztül, miközben egy segédtáblázat elemeit módosítgatjuk. A segédtáblázat 3 oszlopból és annyi sorból áll, ahány úton el lehet jutni a nevezetes állapotba a kiinduló állapotból (ezt az értéket tehát már ismerjük). A segédtáblázat első sora végesautomata állapotokat, a második út darabszámokat, a harmadik szótővégződéseket tartalmaz. Az algoritmus kezdetekor a táblázat csak egy sora van kitöltve a (nevezetes állapot-utak száma-üres sztring) értékekkel. A táblázat oszlopainak értelmezése a következő:
A szófát az eredeti definíciótól kicsit eltérően ábrázoljuk. Ezt az eltérést mutatja az alábbi ábra.
Ahogy a szófába szúrjuk be a szavakat, úgy nő a szófa mérete. A meret tartalmazza az aktuális méretet, a masolasfaktor mondja meg, hogy ha a szófának lefoglalt terület megtelt, akkor még hány elem számára foglaljunk le területet, a meretkorlat pedig azt adja meg, hogy mekkora terület van lefoglalva. Nyilván a masolasfaktor minél nagyobb, annál ritkábban kell újabb területet lefoglalni, tehát a program futása is gyorsabb lesz. A fölöslegesen lefoglalt területet, miután a fájl összes szavát felvette a szófába, a program felszabadítja. Ezért, ha a program gyorsítása érdekében nagy masolasfaktor értéket adunk meg, akkor csak a fájl feldolgozása alatt fog a program több memóriát fogyasztani.
A szófa osztály fontosabb tagfüggvényei a következők:
A végesautomata állapotait és a hozzájuk tarozó éleket ugyanúgy két változó sorhosszúságú tömbben tároljuk, mint a szófánál. A különbség pusztán annyi, hogy a kartomb[i][j]-hez tartozó él az allapottomb[i][j] állapotába mutat. A végesautomatánál ugyanis az allapottomb[i][0] elemében tároljuk, hogy az állapothoz hány úton lehet eljutni a kiinduló állapotból. Azt hogy egy állapotból, hány levélbe vezet él, tehát, hogy hány rag tartozik az állapothoz, a leveltomb-ben tároljuk. A szótő és ragszám tömbjeinek feltöltését, a csak a szófa osztály számára hozzáférhető void szotoszamtolt() és a void leveltombtolt() végzik.
Ahogy a végesautomatába szúrjuk be az állapotokat, úgy nő a végesautomata mérete. A meret tartalmazza az aktuális méretet, a masolasfaktor mondja meg, hogy ha a végesautomatának lefoglalt terület megtelt, akkor még hány elem számára foglaljunk le területet. Nyilván a masolasfaktor minél nagyobb, annál ritkábban kell újabb területet lefoglalni, tehát a program futása is gyorsabb lesz. A fölöslegesen lefoglalt területet, miután a végesautomata összes állapotát felvettük, a void foloslegesvag() függvénnyel lehet felszabadítani. A masolasfaktor nagysága, a program futási idejének, és memória szükségletének kapcsolata, megegyezik a szófánál tárgyalttal.
A végesautomata osztály fontosabb tagfüggvényei a következők: