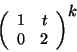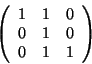Bevezetés a számításelméletbe I.
Vizsgazárthelyi feladatok
2000. december 18.
- Legyen
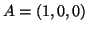 ,
, 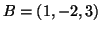 két pont, a
két pont, a 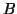 ponton átmenő
ponton átmenő
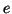 egyenes egyenlete
egyenes egyenlete
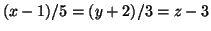 .
Keressük meg az
.
Keressük meg az 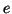 egyenesen azokat a pontokat, melyekre az
egyenesen azokat a pontokat, melyekre az
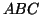 háromszögben
háromszögben
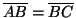 teljesül!
teljesül!
- A kétezredik komplex egységgyökök közül hány olyan van, melynek
az ezredik hatványa is eggyel egyenlő?
- Igazoljuk, hogy ha az
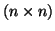 -es
-es 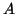 mátrixnak minden
eleme
mátrixnak minden
eleme 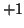 vagy
vagy 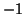 , akkor
, akkor 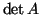 osztható
osztható
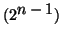 -gyel!
-gyel!
- Egy
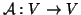 lineáris transzformáció
vetítés, ha
lineáris transzformáció
vetítés, ha
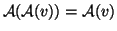 teljesül minden
teljesül minden
 vektorra.
Adjunk példát olyan vetítésre, melynek mátrixához tartozó
kvadratikus alak pozitív szemidefinit!
vektorra.
Adjunk példát olyan vetítésre, melynek mátrixához tartozó
kvadratikus alak pozitív szemidefinit!
- Tekintsük a síkon azon négyzetek halmazát, melyeknek legalább
az egyik csúcsa egész koordinátájú
(a pont mindkét koordinátája egész szám).
Mennyi ennek a halmaznak a számossága?
- Mennyi az
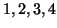 számjegyekből előállítható olyan
négyjegyű számok összege, melyekben mindegyik számjegy pontosan
egyszer fordul elő?
számjegyekből előállítható olyan
négyjegyű számok összege, melyekben mindegyik számjegy pontosan
egyszer fordul elő?
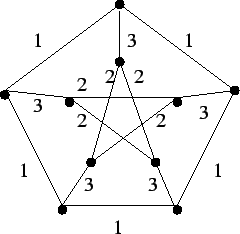
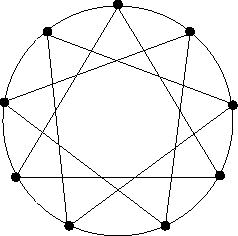
- Határozzuk meg hogy az alábbi gráfban hány különböző
minimális súlyú feszítőfa található!
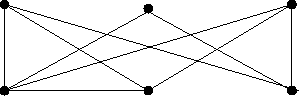
- Síkbarajzolható-e az alábbi gráf? Ha igen rajzoljuk le úgy
a síkba, hogy élei egyenes szakaszok legyenek, ha
nem rajzolható síkba, bizonyítsuk ezt be.
Bevezetés a számításelméletbe I.
Vizsgazárthelyi feladatok
2001. január 2.
- Legyen
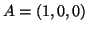 ,
, 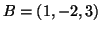 ,
, 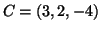 a tér három pontja.
Melyik az a
a tér három pontja.
Melyik az a 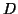 pont, melyre az
pont, melyre az 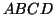 négyszög parallelogramma?
négyszög parallelogramma?
- Mely komplex számokra teljesül a
egyenlet?
- Tetszőleges valós
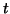 számra és tetszőleges pozitív egész
számra és tetszőleges pozitív egész 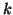 számra számítsuk ki az
számra számítsuk ki az
mátrixot!
- Határozzuk meg az
mátrix sajátértékeit és a hozzájuk tartozó sajátaltereket!
- Mennyi az olyan végtelen hosszú
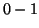 sorozatok halmazának
számossága, melyekben pontosan 5 darab egyes fordul elő?
sorozatok halmazának
számossága, melyekben pontosan 5 darab egyes fordul elő?
- Hány hatra végződő néggyel osztható ötjegyű szám van?
- Ketten a következő játékot játszák.
Adott
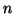 pont, kezdetben semelyik kettő nincs összekötve.
A játékosok felváltva lépnek, minden lépésben a soron következő
játékos az
pont, kezdetben semelyik kettő nincs összekötve.
A játékosok felváltva lépnek, minden lépésben a soron következő
játékos az 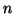 pont közül két tetszőlegesen választott közé behúz
egy élet. Az veszít, aki egy olyan élet húz be,
amitől a gráfban kör keletkezik.
A kezdő vagy a másodiknak lépő játékos fog nyerni, ha feltesszük,
hogy mindketten a lehető legjobban játszanak?
pont közül két tetszőlegesen választott közé behúz
egy élet. Az veszít, aki egy olyan élet húz be,
amitől a gráfban kör keletkezik.
A kezdő vagy a másodiknak lépő játékos fog nyerni, ha feltesszük,
hogy mindketten a lehető legjobban játszanak?
- Van-e olyan 9 pontú
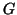 gráf, hogy sem
gráf, hogy sem 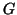 , sem a komplementere
, sem a komplementere
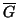 nem síkbarajzolható?
nem síkbarajzolható?
Bevezetés a számításelméletbe I.
Vizsgazárthelyi feladatok
2001. január 15.
- Számítsuk ki az
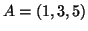 , a
, a 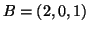 és a
és a 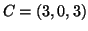 pontok által meghatározott háromszög
pontok által meghatározott háromszög 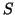 súlypontját!
Határozzuk meg a térnek azon pontjait, melyek rajta vannak az ABC síkra
az
súlypontját!
Határozzuk meg a térnek azon pontjait, melyek rajta vannak az ABC síkra
az 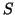 pontban állított merőleges egyenesen!
pontban állított merőleges egyenesen!
- A kétezredik komplex egységgyökök között hány olyan van, melynek
az ötödik hatványa nem egyenlő eggyel?
- Mennyi az
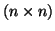 -es
-es 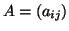 mátrix determinánsa, ha
mátrix determinánsa, ha
- Legyen
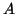 egy
egy 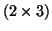 -as mátrix és legyen
-as mátrix és legyen 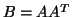 .
Bizonyítsuk be, hogy a
.
Bizonyítsuk be, hogy a 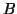 -hez tartozó kvadratikus alak pozitív
definit vagy pozitív szemidefinit. Adjunk példát olyan
-hez tartozó kvadratikus alak pozitív
definit vagy pozitív szemidefinit. Adjunk példát olyan 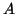 -ra, amikor
-ra, amikor
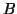 pozitív definit és olyan
pozitív definit és olyan 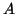 -ra is,
amikor
-ra is,
amikor 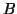 pozitív szemidefinit de nem pozitív definit!
pozitív szemidefinit de nem pozitív definit!
- Mennyi az olyan nullával kezdődő végtelen hosszú sorozatok halmazának
számossága, melyekben bármely két szomszédos tag különbsége
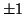 ?
?
- Hányféleképpen tölthették ki azt a lottószelvényt, amelyen pontosan három
találat volt? (A lottón 90 számból húztak ki 5 számot.)
- A
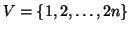 (számozott) pontokon hány olyan
egyszerű
(számozott) pontokon hány olyan
egyszerű 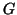 gráf adható meg, melynek
gráf adható meg, melynek 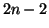 éle van és két
egyforma méretű összefüggő komponensből áll?
éle van és két
egyforma méretű összefüggő komponensből áll?
- Síkbarajzolható-e az alábbi gráf? Ha igen rajzoljuk le úgy
a síkba, hogy élei egyenes szakaszok legyenek, ha
nem rajzolható síkba, bizonyítsuk ezt be.