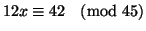Bevezetés a számításelméletbe II. Zárthelyi
feladatok
2000. április 6.
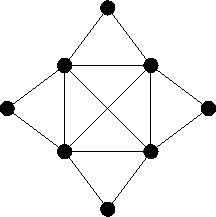
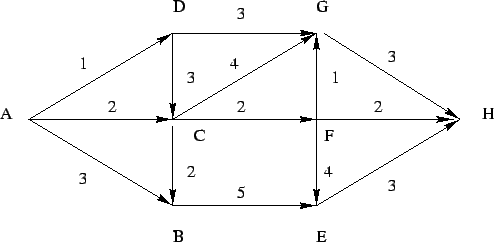
- Minimálisan hányszor kell ``felemelni'' a ceruzát az alábbi ábrán látható
gráf lerajzolásakor, ha minden élet csak egyszer rajzolhatunk meg?
(Egyéb vonalakat nem rajzolhatunk.)
- Igaz-e, hogy ha egy páros gráfban van Hamilton-kör, akkor teljes
párosítást is tartalmaz?
- Egy társaságban bármely két embernek legalább két közös ismerőse van.
Tudjuk továbbá, hogy bármely két ember vagy ismeri egymást, vagy ha nem,
akkor a társaság bármely harmadik tagját legalább az egyikük ismeri.
Bizonyítsuk be, hogy a társaság tagjai leültethetők egy (megfelelő méretű)
kerek asztal köré úgy, hogy mindenki két ismerőse között üljön.
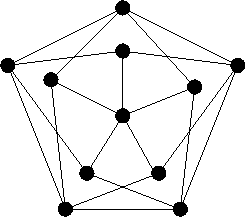
- Állapítsuk meg, hogy mennyi az alábbi ábrán látható
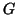 gráf összes
élét lefogó pontok
gráf összes
élét lefogó pontok 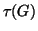 minimális száma.
minimális száma.
- Adjuk meg az összes olyan véges egyszerű gráfot, amire
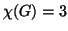 és tetszőleges
és tetszőleges 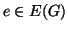 élre
élre
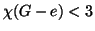 .
.
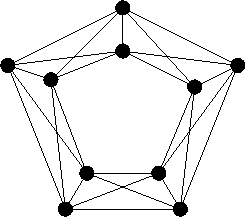
- Mennyi az ábrán látható gráf kromatikus száma?
- Állapítsuk meg, hogy mennyi a feladat elvégzéséhez minimálisan szükséges
idő az alábbi PERT diagram által leírt munkafolyamatnál!
- Legyen
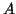 a
a 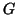 véges egyszerű irányítatlan gráf szomszédossági
mátrixa,
véges egyszerű irányítatlan gráf szomszédossági
mátrixa, 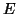 pedig az
pedig az 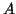 -val azonos méretű egységmátrix.
Bizonyítsuk be, hogy a
-val azonos méretű egységmátrix.
Bizonyítsuk be, hogy a 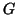 gráfban található legnagyobb független
ponthalmaz
gráfban található legnagyobb független
ponthalmaz 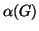 mérete és az
mérete és az 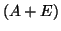 mátrix
mátrix
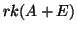 rangja között fönnáll az
rangja között fönnáll az
összefüggés.
Bevezetés a számításelméletbe II. Zárthelyi
feladatok
2000. május 4.
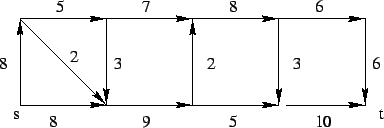
- Adjunk meg az alábbi hálózatban egy maximális folyamot!
- Bizonyítsuk be, hogy ha a
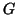 véges egyszeru gráf síkgráf,
akkor
véges egyszeru gráf síkgráf,
akkor 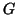 nem lehet hatszorosan (csúcs)összefüggo.
nem lehet hatszorosan (csúcs)összefüggo.
- Egy
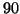 fos társaságból bizonyos párok leveleznek
egymással. Akárhogyan választunk ki közülük tíz embert, ezek
között mindig van legalább ketto, akik leveleznek egymással.
Bizonyítsuk be, hogy a levelezo párok száma legalább
fos társaságból bizonyos párok leveleznek
egymással. Akárhogyan választunk ki közülük tíz embert, ezek
között mindig van legalább ketto, akik leveleznek egymással.
Bizonyítsuk be, hogy a levelezo párok száma legalább 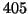 .
.
- Bizonyítsuk be, hogy
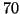 ember között mindig van vagy
ember között mindig van vagy 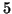 olyan,
akik páronként tegezodnek egymással, vagy
olyan,
akik páronként tegezodnek egymással, vagy 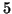 olyan, akik
páronként magázódnak. (Feltesszük, hogy a tegezodés és a
magázódás is kölcsönös, és azt is, hogy bármely két ember
vagy tegezodik, vagy magázódik.)
olyan, akik
páronként magázódnak. (Feltesszük, hogy a tegezodés és a
magázódás is kölcsönös, és azt is, hogy bármely két ember
vagy tegezodik, vagy magázódik.)
- Bizonyítsuk be, hogy négy egymást követo pozitív egész
szám között mindig van olyan, amelyik a másik három mindegyikéhez
(külön-külön) relatív prím.
- Legyenek
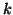 és
és 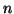 olyan pozitív egészek, amelyekre
olyan pozitív egészek, amelyekre 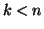 .
Mi a legnagyobb közös osztója az
.
Mi a legnagyobb közös osztója az 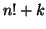 és az
és az 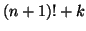 számoknak?
számoknak?
- Legyenek
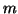 és
és 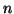 olyan pozitív egészek, amelyekre
olyan pozitív egészek, amelyekre 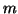 osztója
osztója
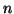 -nek. Bizonyítsuk be, hogy
-nek. Bizonyítsuk be, hogy 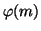 osztója
osztója 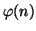 -nek.
-nek.
- Milyen maradékot adhat 45-tel osztva az
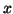 szám, ha
szám, ha