Algoritmuselmélet zárthelyi, 1999. november 18. 1. Egy UNIÓ-HOLVAN adatszerkezetünk van, melynek az S alaphalmaza a magyar abc betuibol áll és amelyben a HOLVAN muveletek során útösszenyomást alkalmazunk. Ennek két fája látható az alábbi rajzon. Rajzolja le az UNIÓ(HOLVAN(G),HOLVAN(L)) végrehajtása után kialakuló helyzetet. 2. Az egészelemu A[1:n] tömböt majdnem rendezettnek nevezünk, ha A[i]>A[j] teljesül minden i-j>5 esetén. Mekkora lesz a beszúrásos rendezés költsége (összehasonlítások, illetve mozgatások száma), ha a bemeneti tömb majdnem rendezett? Mutassa meg, hogy a beszúrásos rendezés algoritmusának kis módosításával az ilyen tömbök lineáris idoben (O(n) összehasonlítás, mozgatás) rendezhetok. 3. Legyen G éllistával adott, súlyozott élu irányított gráf és s egy rögzített csúcsa. Tegyük fel, hogy az élsúlyok nemnegatívak. Javasoljon hatékony algoritmust, mely a G minden v csúcsára megadja a legrövidebb s-bol induló és s-be érkezo olyan irányított séta hosszát, amely a v ponton is átmegy. A séták egy ponton többször is átmehetnek. Elemezze módszere költségét. 4. Adott egy n-pontú bináris fa a szokásos módon (a csúcsokban jobb és bal mutatóval). A csúcsokban tárolt elemek egész számok. Vázoljon O(n) lépésszámú módszert annak az eldöntésére, hogy a fa eleget tesz-e a keresofa-tulajdonságnak. 5. Legyen G egy súlyozott élu, összefüggo, irányítatlan gráf. Tegyük fel, hogy nincs két azonos élsúly, és jelölje F a G (egyetlen) minimális költségu feszítofáját. Igaz-e, hogy az (a) állításból következik a (b) állítás? A két állítás a következo: (a) Minden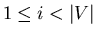 $1\leq i< \vert V\vert$ esetén az F fa i legkisebb éle által feszített részgráf is fa. (b) G-re alkalmazva a Boruvka-algoritmus egy menetben befejezodik. 6. Van a memóriában egy ismeretlen hosszú láncolt lista: a lista minden egyes elemébol egy mutató mutat a következore, kivéve a lista utolsó tagját, ahol a mutató vagy NULL, vagy pedig a lista valamelyik korábbi elemére mutat. (Képzeljétek el a fenti szituációt, mert a rajzot nem tudom berakni most.) Adott a lista elso elemére egy mutató. Vázoljon egy algoritmust, amely a lista (ismeretlen) hosszában mérve lineáris idoben megkülönbözteti a két esetet (vagy megtalalálja a NULL mutatót, vagy pedig felismeri, hogy visszavezeto mutató van.) A listában levo elemeket nem szabad megváltoztatni. A felhasznált munkaterületünkön konstans sok mutatót illetve természetes számot tárolhatunk. A megoldásokhoz megfelelo indoklást kérünk. Jó munkát!